EdinburghModeling

From 2006.igem.org

(Difference between revisions)
Jump to: navigation, search
(→System Diagram of Arsenic Biosensor([http://2006.igem.org/Image:Modeling_the_Arsenic_Biosensor_System.pdf PDF version]))
 
(134 intermediate revisions not shown)
Line 1: Line 1:
-
[http://2006.igem.org/Arsenic_Sensor_Model Arsenic Sensor Model]
+
== Modeling the Arsenic Biosensor System([http://2006.igem.org/Image:Modeling_the_Arsenic_Biosensor_System.pdf PDF version])==
 +
 
 +
==Abstract==
 +
This section reports the modeling progress of an arsenic biosensor system, which is the iGEM project accomplished in the University of Edinburgh 2006. The arsenic biosensor system sought to address the fatal water pollution problem occurring in many poor countries/areas like Bangladesh by producing a calibratable pH changes in response to a range of arsenic concentrations. A computational model which contains 3 operons, 19 reactions and 17 species has been constructed to shed light on the wet-lab experimental design. By analyzing the sensitivity of each parameter/species, we identified their relative importance in the system which gives the theoretical guide when measuring the variable in wet-lab. The next step research is to refine the model by comparing it with the biological output.
 +
 
 +
==Methodology==
 +
The gene expression reactions are modeled using Michaelis-Menten equation while the other reactions are described in Mass-Action equations.
 +
 
 +
We divided the whole system into three operons, namely Urease operon, LambdaCI operon and LacZ operon.
 +
 
 +
(1)The Urease operon:
 +
 
 +
[[Image:EdinUrease_Operon.JPG|600 px]]
 +
 
 +
LacI works as the repressor of Urease through occupying the free binding site of Urease promoter. However, when there is allolactose in the operon, LacI binds to allolactose to form complex with higher affinity. One assumption we made here is that there is sufficient allolactose in the system, so Urease is always being produced in this operon.
 +
 
 +
The reactions which involved in Urease operon is summed up as below.
 +
 
 +
[[Image:EdinUreaseReaction.JPG]]
 +
 
 +
(2)LambdaCI Operon:
 +
 
 +
[[Image:EdinLamdabCI_Operon.JPG|600 px]]
 +
 
 +
LambdaCI operon responses to low concentration of arsenic, e.g., 5ppb. Similar with Urease operon, ArsR represses both LambdaCI and itself (negative feedback loop) through binding site competition. When arsenic presents in the system, ArsR binds to it with affinity higher than it binds to the promoter. That means with arsenic input, LambdaCI is produced and represses the Urease operon through occupying the free binding site of Urease promoter.
 +
 
 +
The reactions involved in LambdaCI operon are summarized as below:
 +
 
 +
[[Image:EdinLambdaCIReaction.JPG]]
 +
 
 +
(3)LacZ operon:
 +
 
 +
[[Image:EdinLacZ_operon.JPG|600 px]]
 +
 
 +
The LacZ operon works in the similar mechanism as LambdaCI operon, but it responses to higher concentration of arsenic, e.g., 20pppb. ArsD represses LacZ and itself until high concentration of arsenic presents in the system. In other words, when there is high concentration of arsenic input, this operon will produce LacZ as output.
 +
 
 +
The reactions involved in this operon are summed up as below:
 +
 
 +
[[Image:EdinLacZ_Reaction.JPG]]
 +
 
 +
Assemble three operons into a whole system
 +
 
 +
[[Image:Model_Diagram2.JPG|600 px]]
 +
 
 +
After three operons have been constructed and tested, they are assembled into the whole arsenic biosensor system. The system works follows the principles as:
 +
 
 +
1) When there is no arsenic input, only Urease operon works and produces Urease as the system output.
 +
 
 +
2) When there is low concentration of arsenic, Urease and LambdaCI operons work and produce Urease and LambdaCI. Because LambdaCI represses the production of Urease, the concentration of Urease is lower than no arsenic condition.
 +
 
 +
3) When the concentration of arsenic rises to high level, all three operons work together. LacZ is produced together with Urease.
 +
 
 +
The complete reaction set is given with the initial condition bellow:
 +
{|border=1
 +
| No. || Name || Equation || Rate Law ||Parameters
 +
|-
 +
|1 ||ArsD binding to Arsenic (III) ||ArsD+2As(III)=ArsD-2As(III)||Mass Action|| K1=1000 K-1=0.65
 +
|-
 +
|2 ||ArsD binding to promoter1  ||2 ArsD+promoter1=2ArsD-promoter1 || Mass Action||K2=10000, K-2=0.65
 +
|-
 +
|3 ||ArsD degradation ||ArsD->null|| Mass Action||K3=0.05
 +
|-
 +
|4 ||ArsD production ||promoter1->promoter1+ArsD||Michaelis-Menten ||V4m=0.5, K4m=75
 +
|-
 +
|5 ||ArsR binding to Arsenic (III) ||ArsR+2As(III)=ArsR-2As(III) ||Mass Action ||K5=1000, K-5=0.65
 +
|-
 +
|6 ||ArsR binding to promoter2 ||2ArsR+promoter2=2ArsR-promoter2 ||Mass Action ||K6=10000, K-6=0.65
 +
|-
 +
|7 ||ArsR degradation ||ArsR->null  ||Mass Action ||K7=0.05
 +
|-
 +
|8 ||ArsR production ||promoter2->promoter2+ArsR ||Michaelis-Menten ||V8m=10, K8m=25
 +
|-
 +
|9 ||LacI binding to allolactose ||LacI+allolactose=LacI-allolactose ||Mass Action ||K9=10000, K-9=0.1
 +
|-
 +
|10 ||LacI binding to promoter4 ||LacI+promoter4 = LacI-promoter4 ||Mass Action ||K10=1000, K-10=0.5
 +
|-
 +
|11 ||LacI degradation ||LacI->null  ||Mass Action ||K11=0.1
 +
|-
 +
|12 ||LacI production ||promoter3->promoter3+LacI ||Michaelis-Menten ||V12m=0.5, K12m=40
 +
|-
 +
|13 ||lacZ degradation ||lacZ->null  ||Mass Action ||K13=0.1
 +
|-
 +
|14 ||lacZ production ||promoter1->promoter1+lacZ ||Michaelis-Menten ||V14m=25, K14m=10
 +
|-
 +
|15 ||LCI binding to promoter 4 ||LCI+promoter4=LCI-promoter4 ||Mass Action ||K15=10000, K-15=0.5
 +
|-
 +
|16 ||LCI degradation ||LCI->null  ||Mass Action ||K16=0.1
 +
|-
 +
|17 ||LCI production ||promoter2->promoter2+LCI ||Michaelis-Menten ||V17m=10, K17m=25
 +
|-
 +
|18 ||Urease degradation ||Urease->null  ||Mass Action ||K18=0.1
 +
|-
 +
|19 ||Urease production ||promoter4->promoter4+Urease ||Michaelis-Menten ||V19m=10, K19m=40
 +
|}
 +
Note: The units for first, second and third order rate constants are expressed in units of second^-1, nMol^-1*second^-1 and nMol^-2*second^-1 respectively.
 +
 
 +
[[Image:Reaction_Map.JPG]]
 +
 
 +
This reaction map is generated from the reaction set above using Simbiology Toolbox.
 +
 
 +
=== Initial concentration ===
 +
{|border=1
 +
| No. || Species || Intial Concentration (nMol)
 +
|-
 +
|1 ||ArsD ||25
 +
|-
 +
|2 ||As(III) ||40
 +
|-
 +
|3 ||2ArsD-promoter1 ||25
 +
|-
 +
|4 ||promoter1 ||5
 +
|-
 +
|5 ||ArsR ||25
 +
|-
 +
|6 ||2ArsR-promoter2 ||25
 +
|-
 +
|7 ||promoter2 ||5
 +
|-
 +
|8 ||LCI ||4
 +
|-
 +
|9 ||LacI ||0.1
 +
|-
 +
|10 ||LacI-allolactose ||0.1
 +
|-
 +
|11 ||allolactose ||1000
 +
|-
 +
|12 ||LacI-promoter4 ||0.1
 +
|-
 +
|13 ||promoter4 ||25
 +
|-
 +
|14 ||LCI-promoter4 ||0.1
 +
|-
 +
|15 ||Urease ||0.1
 +
|-
 +
|16 ||promoter3 ||5
 +
|-
 +
|17 ||Other species ||0
 +
|}
 +
 
 +
===Ordinary Differential Equation===
 +
[[Image:EdinOde1.JPG|800 px]]
 +
[[Image:EdinOde2.JPG|800 px]]
 +
 
 +
===Software used===
 +
In order to model the quantitative behaviour of the dynamic system, many modeling
 +
software systems have been developed in the past few years. In this project, three kinds of software systems are used for modelling. This section introduces their functions and features.
 +
 
 +
1.System biology toolbox for Matlab: SimBiology toolbox provides functions for
 +
modelling, simulating, and analysing biochemical pathways on basis of the powerful computing engine of Matlab. Aside from the conventional typing reaction equation, SimBiology provides a user-friendly ‘dragging-and-dropping’ block diagram editor to build a new model. Thanks to the powerful computing ability of Matlab, SimBiology integrates a wide range of numerical solvers for both stochastic and deterministic simulations. Another strength of SimBiology is its analysing ability which includes sensitivity analysis, parameter estimation and conservation of moieties. Last but not the least, SimBiology provides user-defined plotting function which was widely used in this research project. However SimBiology is commercial software, it costs the budgeted researchers extra expense to purchase the license for this toolbox. Also, there is no GUI for sensitivity analysis and parameters scan functions, so users should obtain the skill of programming with Matlab.
 +
 
 +
2.BIOCHAM: BIOCHAM stands for biochemical abstract machine which is a formal modeling environment for system biology. Because of its rule-based language and temporal logic based language, BIOCHAM can offer an automatically reasoning tool for querying the temporal properties of the system under all its possible behaviours. It is very useful for constructing models especially when numerical data is unavailable. BIOCHAM also provides a state-of-the-art symbolic model checker for handling the complexity of large highly non-deterministic models. Furthermore, it provides simulation results via its graphical interface. One disadvantage of BIOCHAM is that because it is initially developed under UNIX, it uses command line rather than GUI to build new models, requiring users to write scripts by hand. Another problem was that when transplanting the program from UNIX to Windows, the model checker of NuSMV does not work well. So this project used BIOCHAM in Fedora 5 rather than Windows XP.
 +
 
 +
3. COPASI: COPASI is freeware developed with collaboration of VBI and EMLR. It provides almost the same functions as SimBiology, though not quite powerful. But compared with SimBiology, it provides a friendly user interface for model analysis, such as parameter estimation, and parameter scan. But there is no parameters/species sensitivity analysis function in COPASI, and also it is not very stable in use, crashing without any responses.
 +
 
 +
To sum up, each software has its own pros and cons. A good strategy is to apply
 +
them for different purposes, for example, using SimBiology to analyze the sensitivity of the model, and using COPASI to scan the most sensitive parameters. When logical queries are needed, BIOCHAM should be the first choice. SimBiology is suitable for generating professional plots, however due to the license requirement, COPASI can be the alternative choice to to run simulations and export the results to such plotting software as SigmaPlot.
 +
 
 +
==Results==
 +
===System response===
 +
 
 +
[[Image:System_output_5ppb.jpg|600 px|thumb|center|Fig.1 System response with 5ppb arsenic input]]
 +
 
 +
When the concentration of arsenic is low, like 5ppb input, the production of Urease is at a high level above 25 units while lacZ production is at a basal level less than 5 units.
 +
 
 +
[[Image:System_output_20ppb.jpg|600 px|thumb|center|Fig.2 System response with 20ppb arsenic input]]
 +
 
 +
When the arsenic concentration rises to higher level like 20ppb, Urease decreases to almost zero because of the repression by LambdaCI and the concentration of lacZ increases to about 10 units because the ArsD has been captured by Arsenic molecules.
 +
 
 +
Because of the different responses of the system, a significant change of pH value is obtained.
 +
 
 +
===Parameter sensitivity analysis===
 +
To provide suggestions to the experimental biologists which proteins or which reaction rates should be measured, it is important to find out the relative importance of each parameter in the system. Parameter sensitivity analysis is used to identify which parameters are more critical in effecting the output of the pathway, and help to gain a deeper insight of the structure and the function of the system.
 +
 
 +
[[Image:Sensitivity_of_lacZ_with_Respect_to_Model_Parameters_1-16.jpg|600 px|thumb|center|Fig.3 Sensitivity of lacZ with Respect to Model Parameters 1-16]]
 +
 
 +
[[Image:Sensitivity_of_lacZ_with_Respect_to_Model_Parameters_17-32.jpg|600 px|thumb|center|Fig.4 Sensitivity of lacZ with Respect to Model Parameters 17-32]]
 +
 
 +
====The most sensitive parameters affecting lacZ====
 +
{|border=1|center
 +
| Nanme || Description ||Peak value of sensitivity || Normal value
 +
|-
 +
|K-1 ||ArsD-2AS(III) dissociate rate ||-2||0.65/s
 +
|-
 +
|K-2 ||2ArsD-promoter1 dissociate rate ||4 ||0.65/s
 +
|-
 +
|K3 ||ArsD degradation rate ||90 ||0.05/s
 +
|-
 +
|K7 ||ArsR degradation rate ||12 ||0.05/s
 +
|-
 +
|K13 ||LacZ degradation rate ||-35 ||0.1/s
 +
|}
 +
 
 +
 
 +
[[Image:Varying_the_Value_of_Parameter_K-1_effect_on_lacZ.jpg|300 px|thumb|center|Fig.5 Varying the Value of Parameter K-1 effect on lacZ]]
 +
 
 +
[[Image:Varying_the_Value_of_Parameter_K-1_effect_on_lacZ_(3D).JPG|300 px|thumb|center|Fig.6 Varying the Value of Parameter K-1 effect on lacZ (3D)]]
 +
 
 +
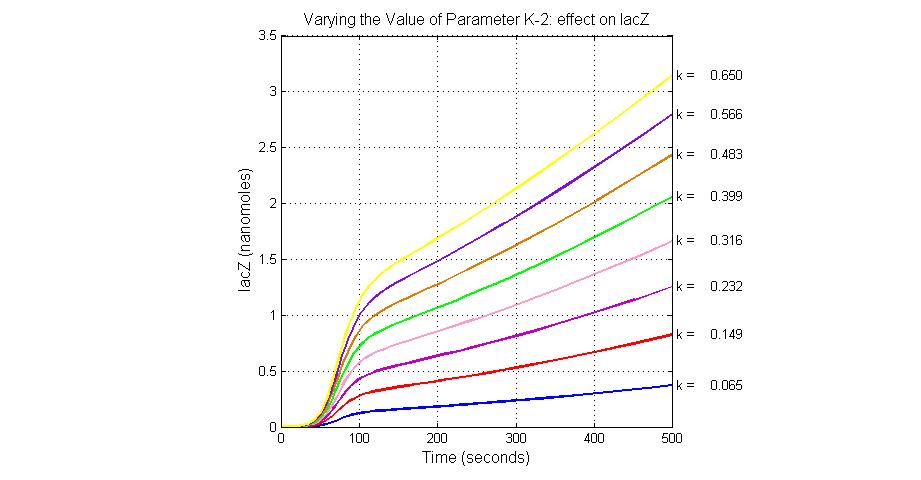
[[Image:Varying_the_Value_of_Parameter_K-2_effect_on_lacZ.jpg|300 px|thumb|center|Fig.7 Varying the Value of Parameter K-2 effect on lacZ]]
 +
 
 +
 
 +
[[Image:Varying_the_Value_of_Parameter_K3_effect_on_lacZ.jpg|300 px|thumb|center|Fig.8 Varying the Value of Parameter K3 effect on lacZ]]
 +
 
 +
[[Image:Varying_the_Value_of_Parameter_K7_effect_on_lacZ.jpg|300 px|thumb|center|Fig.9 Varying the Value of Parameter K7 effect on lacZ]]
 +
 
 +
[[Image:Varying_the_Value_of_Parameter_K13_effect_on_lacZ.jpg|300 px|thumb|center|Fig.10 Varying the Value of Parameter K13 effect on lacZ]]
 +
 
 +
[[Image:Sensitivity_of_Urease_with_Respect_to_Model_Parameters_1-16.jpg|600 px|thumb|center|Fig.11 Sensitivity of Urease with Respect to Model Parameters 1-16]]
 +
 
 +
[[Image:Sensitivity_of_Urease_with_Respect_to_Model_Parameters_17-32.jpg|600 px|center|thumb|Fig.12 Sensitivity of Urease with Respect to Model Parameters 17-32]]
 +
 
 +
====The most sensitive parameters affecting Urease====
 +
{|border=1|center
 +
| Nanme || Description ||Peak value of sensitivity || Normal value
 +
|-
 +
|k3 ||ArsD degradation rate ||-30||0.05/s
 +
|-
 +
|k-6 ||2ArsR-promoter2 dissociate rate ||-5 ||0.65/s
 +
|-
 +
|k7 ||ArsR degradation rate ||-120 ||0.05/s
 +
|-
 +
|K18 ||Urease degradation rate ||-350  ||0.1/s
 +
|-
 +
|V19m ||Urease production maxium rate ||3.5 ||10 nMol/s
 +
|}
 +
 
 +
[[Image:Varying_the_Value_of_Parameter_K3_effect_on_Urease.jpg|300 px|thumb|center|Fig.13 Varying the Value of Parameter K3 effect on Urease]]
 +
 
 +
[[Image:Varying_the_Value_of_Parameter_K-6_effect_on_Urease.jpg|300 px|thumb|center|Fig.14 Varying the Value of Parameter K-6 effect on Urease]]
 +
 
 +
[[Image:Varying_the_Value_of_Parameter_K7_effect_on_Urease.jpg|300 px|thumb|center|Fig.15 Varying the Value of Parameter K7 effect on Urease]]
 +
 
 +
[[Image:Varying_the_Value_of_Parameter_K18_effect_on_Urease.jpg|300 px|thumb|center|Fig.16 Varying the Value of Parameter K18 effect on Urease]]
 +
 
 +
===Species sensitivity analysis===
 +
[[Image:Sensitivity_of_lacZ_with_Respect_to_Model_Species.jpg|600 px|center|thumb|Fig.7 Sensitivity of lacZ with Respect to Model Species]]
 +
 
 +
====The most sensitive species affecting lacZ====
 +
{|border=1|center
 +
|Name||Initial concentration (nMol)
 +
|-
 +
|promoter1 ||5.0
 +
|-
 +
|promoter2 ||5.0
 +
|-
 +
|ArsD-2As(III) ||0
 +
|-
 +
|ArsD  ||25
 +
|-
 +
|ArsR  ||25
 +
|}
 +
 
 +
[[Image:Varying_the_Value_of_Species_promoter1_Effect_on_lacZ.jpg|300 px|center|thumb|Fig.17 Varying the Value of Species promoter1 Effect on lacZ]]
 +
 
 +
[[Image:Varying_the_Value_of_Species_promoter2_Effect_on_lacZ.jpg|300 px|center|thumb|Fig.18 Varying the Value of Species promoter2 Effect on lacZ]]
 +
 
 +
[[Image:Varying_the_Value_of_Species_ArsD-2As(III)_Effect_on_lacZ.jpg|300 px|center|thumb|Fig.19 Varying the Value of Species ArsD-2As(III) Effect on lacZ]]
 +
 
 +
[[Image:Varying_the_Value_of_Species_ArsD_Effect_on_lacZ.jpg|300 px|center|thumb|Fig.20 Varying the Value of Species ArsD Effect on lacZ]]
 +
 
 +
 
 +
[[Image:Varying_the_Value_of_Species_ArsR_Effect_on_lacZ.jpg|300 px|center|thumb|Fig.21 Varying the Value of Species ArsR Effect on lacZ]]
 +
 
 +
 
 +
[[Image:Sensitivity_of_Urease_with_Respect_to_Model_Species.jpg|600 px|center|thumb|Fig.22 Sensitivity of Urease with Respect to Model Species]]
 +
 
 +
====The most sensitive species affecting Urease====
 +
{|border=1|center
 +
|Name||Initial concentration (nMol)
 +
|-
 +
|LCI ||4
 +
|-
 +
|LacI-promoter4 ||0.1
 +
|-
 +
|promoter4 ||25
 +
|-
 +
|promoter2  ||5
 +
|-
 +
|promoter1 ||5
 +
|}
 +
 
 +
[[Image:Varying_the_Value_of_Species_LCI_Effect_on_Urease.jpg|300 px|center|thumb|Fig.23 Varying the Value of Species LCI Effect on Urease]]
 +
 
 +
[[Image:Varying_the_Value_of_Species_LacI-promoter4_Effect_on_Urease.jpg|300 px|center|thumb|Fig.24 Varying the Value of Species LacI-promoter4 Effect on Urease]]
 +
 
 +
 
 +
[[Image:Varying_the_Value_of_Species_promoter4_Effect_on_Urease.jpg|300 px|center|thumb|Fig.25 Varying the Value of Species promoter4 Effect on Urease]]
 +
 
 +
[[Image:Varying_the_Value_of_Species_promoter2_Effect_on_Urease.jpg|300 px|center|thumb|Fig.26 Varying the Value of Species promoter2 Effect on Urease]]
 +
 
 +
==Appendix==
 +
===Appendix 1. The Matlab scripts for multi-parameter sensitivity analysis===
 +
 
 +
sbioloadproject Biosensor    %change the project name to replace “Biosensor” here
 +
 
 +
m1
 +
 
 +
m1.Species
 +
 
 +
m1.Reactions
 +
 
 +
csObj = getconfigset(m1);
 +
 
 +
% change stop time to the time you want the simulation to run for in the line below
 +
 
 +
set(csObj, 'StopTime', 500);
 +
 
 +
csObj
 +
 
 +
csObj.RunTimeOptions.StatesToLog
 +
 
 +
% in line below change urease for the output you want to monitor
 +
 
 +
csObj.RunTimeOptions.StatesToLog = sbioselect...
 +
(m1, 'type', 'species', 'Where', 'Name', '==', 'Urease');
 +
 
 +
csObj.RunTimeOptions.StatesToLog
 +
 
 +
set(csObj.SolverOptions, 'SensitivityAnalysis', true);
 +
 
 +
pif = [sbioselect(m1, 'Type', 'parameter', 'Where', 'Name', '==', 'K1');...
 +
%change the name of parameter here
 +
 
 +
sbioselect(m1, 'Type', 'parameter', 'Where', 'Name', '==', 'K-1')
 +
 
 +
sbioselect(m1, 'Type', 'parameter', 'Where', 'Name', '==', 'K2')
 +
 
 +
sbioselect(m1, 'Type', 'parameter', 'Where', 'Name', '==', 'K-2')
 +
 
 +
sbioselect(m1, 'Type', 'parameter', 'Where', 'Name', '==', 'K3')
 +
 
 +
sbioselect(m1, 'Type', 'parameter', 'Where', 'Name', '==', 'V4m')
 +
 
 +
sbioselect(m1, 'Type', 'parameter', 'Where', 'Name', '==', 'K4m')
 +
 
 +
sbioselect(m1, 'Type', 'parameter', 'Where', 'Name', '==', 'K5')
 +
 
 +
sbioselect(m1, 'Type', 'parameter', 'Where', 'Name', '==', 'K-5')
 +
 
 +
sbioselect(m1, 'Type', 'parameter', 'Where', 'Name', '==', 'K6')
 +
 
 +
sbioselect(m1, 'Type', 'parameter', 'Where', 'Name', '==', 'K-6')
 +
 
 +
sbioselect(m1, 'Type', 'parameter', 'Where', 'Name', '==', 'K7')
 +
 
 +
sbioselect(m1, 'Type', 'parameter', 'Where', 'Name', '==', 'V8m')
 +
 
 +
sbioselect(m1, 'Type', 'parameter', 'Where', 'Name', '==', 'K8m')
 +
 
 +
sbioselect(m1, 'Type', 'parameter', 'Where', 'Name', '==', 'K9')
 +
 
 +
sbioselect(m1, 'Type', 'parameter', 'Where', 'Name', '==', 'K-9')];
 +
 
 +
set(csObj.SensitivityAnalysisOptions, 'ParameterInputFactors', pif);
 +
 
 +
set(csObj.SensitivityAnalysisOptions, 'Normalization', 'None');
 +
 
 +
warning('off', 'MATLAB:divideByZero');
 +
 
 +
tsObj = sbiosimulate(m1);
 +
 
 +
[T, R, snames, ifacs] = sbiogetsensmatrix(tsObj);
 +
 
 +
size(R)
 +
 
 +
R2 = squeeze(R);
 +
 
 +
figure;
 +
 
 +
plot(T,R2);
 +
 
 +
% in lines below change the labels to suit the graph you want to draw
 +
 
 +
title('Sensitivity of Urease with Respect to Model Parameters 1-16');
 +
 
 +
xlabel('Time (seconds)');
 +
 
 +
ylabel('Sensitivity of Urease');
 +
 
 +
===Appendix 2. The Matlab script for Multi-species sensitivity analysis===
 +
 
 +
sbioloadproject Biosensor
 +
 
 +
m1
 +
 
 +
m1.Species
 +
 
 +
m1.Reactions
 +
 
 +
csObj = getconfigset(m1);
 +
 
 +
% change stop time to the time you want the simulation to run for in the line below
 +
 
 +
set(csObj, 'StopTime', 500);
 +
 
 +
csObj
 +
 
 +
csObj.RunTimeOptions.StatesToLog
 +
 
 +
% in line below change urease for the output you want to monitor
 +
 
 +
csObj.RunTimeOptions.StatesToLog = sbioselect...
 +
(m1, 'type', 'species', 'Where', 'Name', '==', 'Urease');
 +
 
 +
csObj.RunTimeOptions.StatesToLog
 +
 
 +
set(csObj.SolverOptions, 'SensitivityAnalysis', true);
 +
 
 +
sif = [sbioselect(m1, 'Type', 'species', 'Where', 'Name', '==', 'ArsD');...
 +
 
 +
sbioselect(m1, 'Type', 'species', 'Where', 'Name', '==', 'As(III)');...
 +
 
 +
sbioselect(m1, 'Type', 'species', 'Where', 'Name', '==', 'ArsD-2As(III)');...
 +
 
 +
sbioselect(m1, 'Type', 'species', 'Where', 'Name', '==', 'promoter1');...
 +
 
 +
sbioselect(m1, 'Type', 'species', 'Where', 'Name', '==', '2ArsD-promoter1');...
 +
 
 +
sbioselect(m1, 'Type', 'species', 'Where', 'Name', '==', 'ArsR');...
 +
 
 +
sbioselect(m1, 'Type', 'species', 'Where', 'Name', '==', 'ArsR-2As(III)');...
 +
 
 +
sbioselect(m1, 'Type', 'species', 'Where', 'Name', '==', 'promoter2');...
 +
 
 +
sbioselect(m1, 'Type', 'species', 'Where', 'Name', '==', '2ArsR-promoter2');...
 +
 
 +
sbioselect(m1, 'Type', 'species', 'Where', 'Name', '==', 'LacI');...
 +
 
 +
sbioselect(m1, 'Type', 'species', 'Where', 'Name', '==', 'allolactose');...
 +
 
 +
sbioselect(m1, 'Type', 'species', 'Where', 'Name', '==', 'LacI-allolactose');...
 +
 
 +
sbioselect(m1, 'Type', 'species', 'Where', 'Name', '==', 'promoter4');...
 +
 
 +
sbioselect(m1, 'Type', 'species', 'Where', 'Name', '==', 'LacI-promoter4');...
 +
 
 +
sbioselect(m1, 'Type', 'species', 'Where', 'Name', '==', 'promoter3');...
 +
 
 +
sbioselect(m1, 'Type', 'species', 'Where', 'Name', '==', 'lacZ');...
 +
 
 +
sbioselect(m1, 'Type', 'species', 'Where', 'Name', '==', 'LCI');...
 +
 
 +
sbioselect(m1, 'Type', 'species', 'Where', 'Name', '==', 'LCI-promoter4');...
 +
 
 +
sbioselect(m1, 'Type', 'species', 'Where', 'Name', '==', 'Urease')
 +
];
 +
 
 +
set(csObj.SensitivityAnalysisOptions, 'SpeciesInputFactors', sif);
 +
 
 +
set(csObj.SensitivityAnalysisOptions, 'Normalization', 'None');
 +
 
 +
warning('off', 'MATLAB:divideByZero');
 +
 
 +
tsObj = sbiosimulate(m1);
 +
 
 +
[T, R, snames, ifacs] = sbiogetsensmatrix(tsObj);
 +
 
 +
size(R)
 +
 
 +
R2 = squeeze(R);
 +
 
 +
figure;
 +
 
 +
plot(T,R2);
 +
 
 +
% in lines below change the labels to suit the graph you want to draw
 +
 
 +
title('Sensitivity of Urease with Respect to Model Species');
 +
 
 +
xlabel('Time (seconds)');
 +
 
 +
ylabel('Sensitivity of Urease');
 +
 
 +
===Appendix 3. The Matlab lab script for parameter scan===
 +
 
 +
sbioloadproject Tuning
 +
 
 +
m1
 +
 
 +
m1.Species
 +
 
 +
m1.Reactions
 +
 
 +
csObj = getconfigset(m1);
 +
 
 +
% change stop time to the time you want the simulation to run for in the line below
 +
 
 +
set(csObj, 'StopTime', 5000);
 +
 
 +
csObj
 +
 
 +
csObj.RunTimeOptions.StatesToLog
 +
 
 +
% in line below change urease for the output you want to monitor
 +
 
 +
csObj.RunTimeOptions.StatesToLog = sbioselect...
 +
(m1, 'type', 'species', 'Where', 'Name', '==', 'promoter1');
 +
 
 +
set(csObj.SolverOptions, 'SensitivityAnalysis', false);
 +
 
 +
set(csObj.SensitivityAnalysisOptions, 'Normalization', 'None');
 +
 
 +
h1 = figure;
 +
 
 +
ax1 = gca(h1);
 +
 
 +
% in next line change Vm4 to the name of the parameter you want to scan
 +
 
 +
p = sbioselect(m1, 'Type', 'parameter', 'Name', 'K2');
 +
 
 +
% in next line the first number is the lower limit and the second number the upper limit
 +
 
 +
% of your range and the last number is the number of scans in that range
 +
 
 +
s = linspace(1000, 100000, 8);
 +
 
 +
for k = s
 +
 
 +
set(p, 'Value', k);
 +
 
 +
[T,x,names] = sbiosimulate(m1);
 +
 
 +
str = sprintf( ' k = %8.3f',k);
 +
 
 +
plot(ax1,T,x(:,1));
 +
 
 +
figure(h1);
 +
 
 +
hold on;
 +
 
 +
text(T(end),x(end,1),str);
 +
 
 +
end
 +
 
 +
axis([ax1], 'square');
 +
 
 +
% Change these lines to suit your data
 +
 
 +
title(ax1, 'Varying the Value of Parameter K18 effect on Urease');
 +
 
 +
xlabel(ax1, 'Time (seconds)');
 +
 
 +
ylabel(ax1, 'Urease (nanomoles)');
 +
 
 +
===Appendix 4. The Matlab Script for species scan===
 +
 
 +
sbioloadproject Biosensor
 +
 
 +
m1
 +
 
 +
m1.Species
 +
 
 +
m1.Reactions
 +
 
 +
csObj = getconfigset(m1);
 +
 
 +
% change stop time to the time you want the simulation to run for in the line below
 +
 
 +
set(csObj, 'StopTime', 500);
 +
 
 +
csObj
 +
 
 +
csObj.RunTimeOptions.StatesToLog
 +
 
 +
% in line below change urease for the output you want to monitor
 +
 
 +
csObj.RunTimeOptions.StatesToLog = sbioselect...
 +
(m1, 'type', 'species', 'Where', 'Name', '==', 'Urease');
 +
 
 +
set(csObj.SolverOptions, 'SensitivityAnalysis', false);
 +
 
 +
set(csObj.SensitivityAnalysisOptions, 'Normalization', 'None');
 +
 
 +
h1 = figure;
 +
 
 +
ax1 = gca(h1);
 +
 
 +
% in next line change Vm4 to the name of the parameter you want to scan
 +
 
 +
p = sbioselect(m1, 'Type', 'species', 'Name', 'promoter1');
 +
 
 +
% in next line the first number is the lower limit and the second number the upper limit
 +
 
 +
% of your range and the last number is the number of scans in that range
 +
 
 +
s = linspace(0, 50, 8);
 +
 
 +
for spR = s
 +
 
 +
set(p, 'InitialAmount', spR);
 +
 
 +
[T,x,names] = sbiosimulate(m1);
 +
 
 +
str = sprintf( ' R = %8.3f',spR);
 +
 
 +
plot(ax1,T,x(:,1));
 +
 
 +
figure(h1);
 +
 
 +
hold on;
 +
 
 +
text(T(end),x(end,1),str);
 +
 
 +
end
 +
 
 +
axis([ax1], 'square');
 +
 
 +
% Change these lines to suit your data
 +
 
 +
title(ax1, 'Varying the Value of Species promoter1: Effect on Urease');
 +
 
 +
xlabel(ax1, 'Time (seconds)');
 +
 
 +
ylabel(ax1, 'Urease (nanomoles)');
 +
 
 +
__NOTOC__
 +
[http://2006.igem.org/University_of_Edinburgh_2006 Main page]

Latest revision as of 13:42, 29 October 2006

Modeling the Arsenic Biosensor System([http://2006.igem.org/Image:Modeling_the_Arsenic_Biosensor_System.pdf PDF version])

Abstract

This section reports the modeling progress of an arsenic biosensor system, which is the iGEM project accomplished in the University of Edinburgh 2006. The arsenic biosensor system sought to address the fatal water pollution problem occurring in many poor countries/areas like Bangladesh by producing a calibratable pH changes in response to a range of arsenic concentrations. A computational model which contains 3 operons, 19 reactions and 17 species has been constructed to shed light on the wet-lab experimental design. By analyzing the sensitivity of each parameter/species, we identified their relative importance in the system which gives the theoretical guide when measuring the variable in wet-lab. The next step research is to refine the model by comparing it with the biological output.

Methodology

The gene expression reactions are modeled using Michaelis-Menten equation while the other reactions are described in Mass-Action equations.

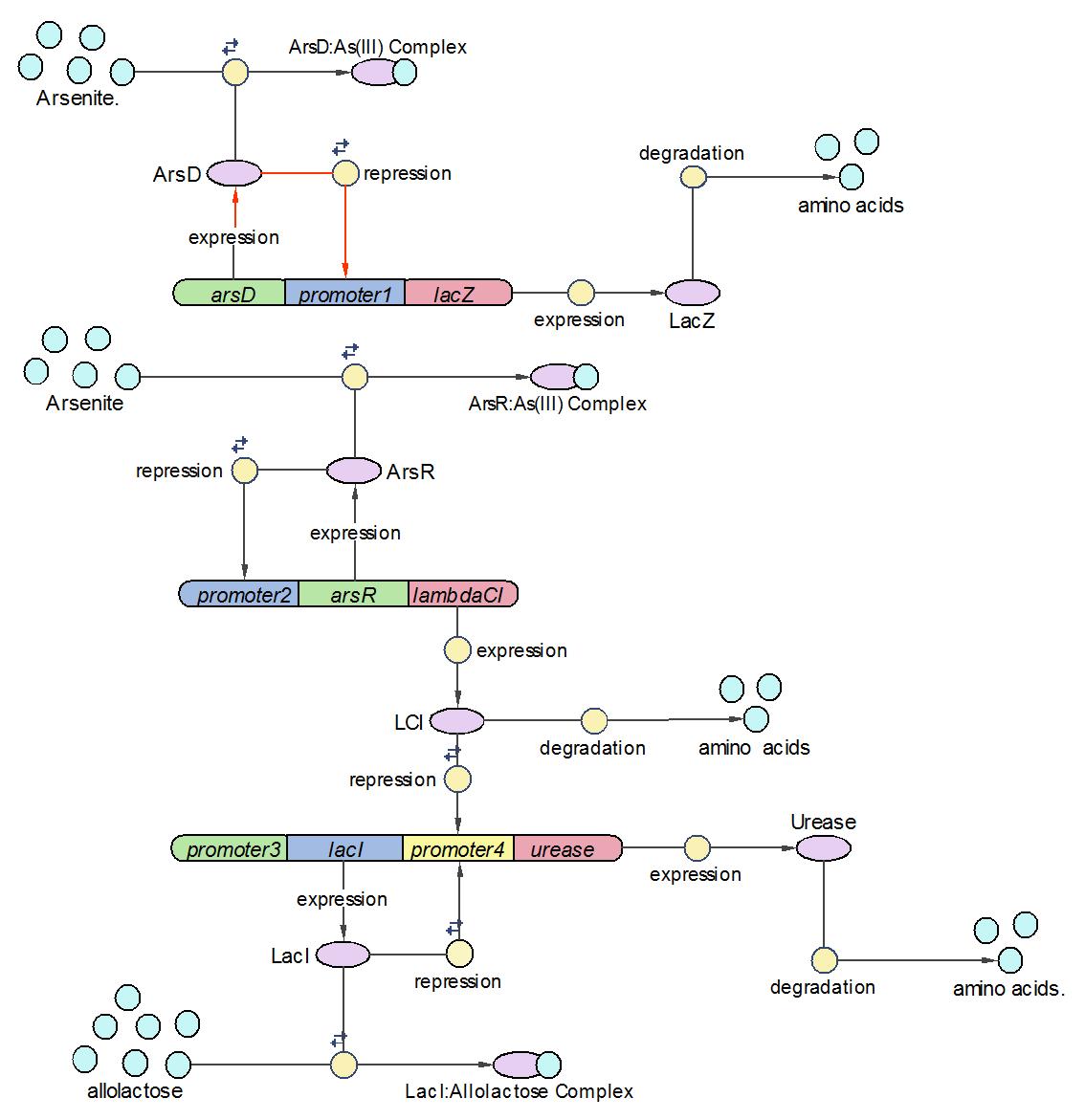
We divided the whole system into three operons, namely Urease operon, LambdaCI operon and LacZ operon.

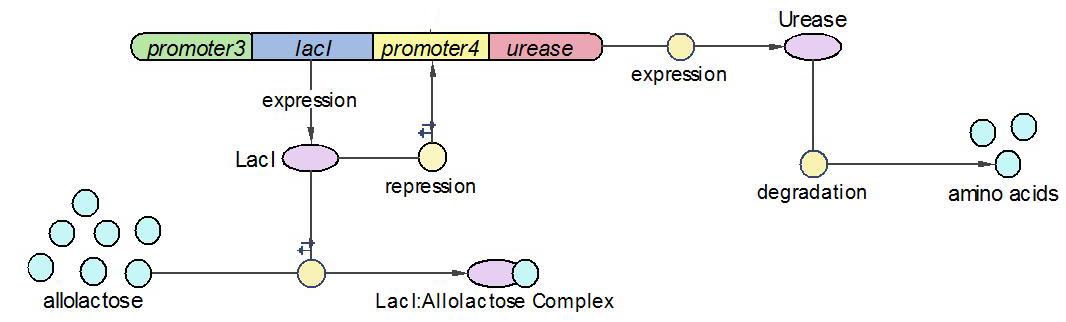
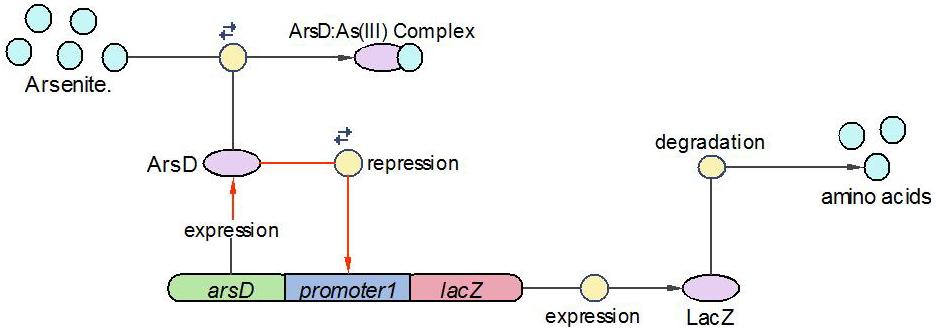
(1)The Urease operon:

EdinUrease Operon.JPG

LacI works as the repressor of Urease through occupying the free binding site of Urease promoter. However, when there is allolactose in the operon, LacI binds to allolactose to form complex with higher affinity. One assumption we made here is that there is sufficient allolactose in the system, so Urease is always being produced in this operon.

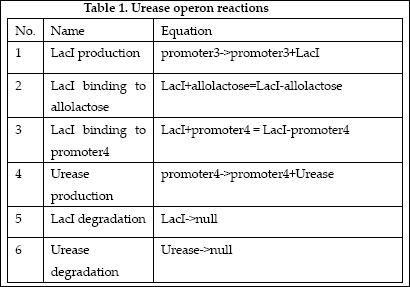
The reactions which involved in Urease operon is summed up as below.

EdinUreaseReaction.JPG

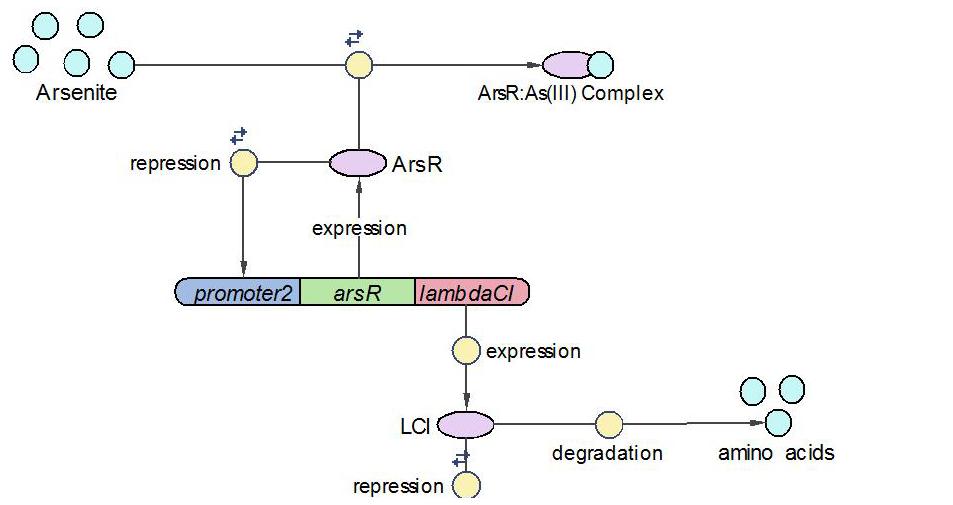
(2)LambdaCI Operon:

EdinLamdabCI Operon.JPG

LambdaCI operon responses to low concentration of arsenic, e.g., 5ppb. Similar with Urease operon, ArsR represses both LambdaCI and itself (negative feedback loop) through binding site competition. When arsenic presents in the system, ArsR binds to it with affinity higher than it binds to the promoter. That means with arsenic input, LambdaCI is produced and represses the Urease operon through occupying the free binding site of Urease promoter.

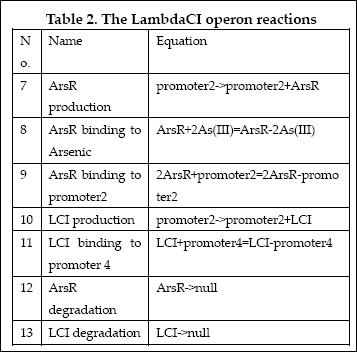
The reactions involved in LambdaCI operon are summarized as below:

EdinLambdaCIReaction.JPG

(3)LacZ operon:

EdinLacZ operon.JPG

The LacZ operon works in the similar mechanism as LambdaCI operon, but it responses to higher concentration of arsenic, e.g., 20pppb. ArsD represses LacZ and itself until high concentration of arsenic presents in the system. In other words, when there is high concentration of arsenic input, this operon will produce LacZ as output.

The reactions involved in this operon are summed up as below:

EdinLacZ Reaction.JPG

Assemble three operons into a whole system

Model Diagram2.JPG

After three operons have been constructed and tested, they are assembled into the whole arsenic biosensor system. The system works follows the principles as:

1) When there is no arsenic input, only Urease operon works and produces Urease as the system output.

2) When there is low concentration of arsenic, Urease and LambdaCI operons work and produce Urease and LambdaCI. Because LambdaCI represses the production of Urease, the concentration of Urease is lower than no arsenic condition.

3) When the concentration of arsenic rises to high level, all three operons work together. LacZ is produced together with Urease.

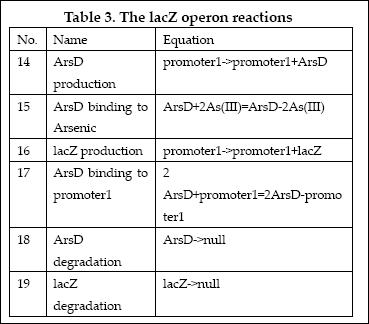
The complete reaction set is given with the initial condition bellow:

No. Name Equation Rate Law Parameters
1 ArsD binding to Arsenic (III) ArsD+2As(III)=ArsD-2As(III)Mass Action K1=1000 K-1=0.65
2 ArsD binding to promoter1 2 ArsD+promoter1=2ArsD-promoter1 Mass ActionK2=10000, K-2=0.65
3 ArsD degradation ArsD->null Mass ActionK3=0.05
4 ArsD production promoter1->promoter1+ArsDMichaelis-Menten V4m=0.5, K4m=75
5 ArsR binding to Arsenic (III) ArsR+2As(III)=ArsR-2As(III) Mass Action K5=1000, K-5=0.65
6 ArsR binding to promoter2 2ArsR+promoter2=2ArsR-promoter2 Mass Action K6=10000, K-6=0.65
7 ArsR degradation ArsR->null Mass Action K7=0.05
8 ArsR production promoter2->promoter2+ArsR Michaelis-Menten V8m=10, K8m=25
9 LacI binding to allolactose LacI+allolactose=LacI-allolactose Mass Action K9=10000, K-9=0.1
10 LacI binding to promoter4 LacI+promoter4 = LacI-promoter4 Mass Action K10=1000, K-10=0.5
11 LacI degradation LacI->null Mass Action K11=0.1
12 LacI production promoter3->promoter3+LacI Michaelis-Menten V12m=0.5, K12m=40
13 lacZ degradation lacZ->null Mass Action K13=0.1
14 lacZ production promoter1->promoter1+lacZ Michaelis-Menten V14m=25, K14m=10
15 LCI binding to promoter 4 LCI+promoter4=LCI-promoter4 Mass Action K15=10000, K-15=0.5
16 LCI degradation LCI->null Mass Action K16=0.1
17 LCI production promoter2->promoter2+LCI Michaelis-Menten V17m=10, K17m=25
18 Urease degradation Urease->null Mass Action K18=0.1
19 Urease production promoter4->promoter4+Urease Michaelis-Menten V19m=10, K19m=40

Note: The units for first, second and third order rate constants are expressed in units of second^-1, nMol^-1*second^-1 and nMol^-2*second^-1 respectively.

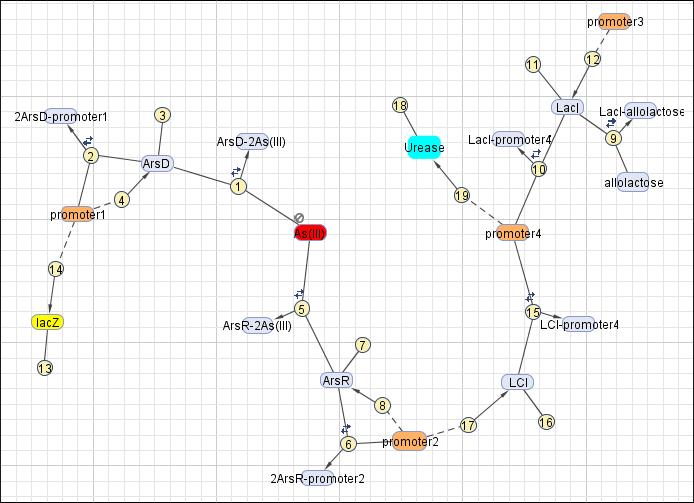
Reaction Map.JPG

This reaction map is generated from the reaction set above using Simbiology Toolbox.

Initial concentration

No. Species Intial Concentration (nMol)
1 ArsD 25
2 As(III) 40
3 2ArsD-promoter1 25
4 promoter1 5
5 ArsR 25
6 2ArsR-promoter2 25
7 promoter2 5
8 LCI 4
9 LacI 0.1
10 LacI-allolactose 0.1
11 allolactose 1000
12 LacI-promoter4 0.1
13 promoter4 25
14 LCI-promoter4 0.1
15 Urease 0.1
16 promoter3 5
17 Other species 0

Ordinary Differential Equation

EdinOde1.JPG EdinOde2.JPG

Software used

In order to model the quantitative behaviour of the dynamic system, many modeling software systems have been developed in the past few years. In this project, three kinds of software systems are used for modelling. This section introduces their functions and features.

1.System biology toolbox for Matlab: SimBiology toolbox provides functions for modelling, simulating, and analysing biochemical pathways on basis of the powerful computing engine of Matlab. Aside from the conventional typing reaction equation, SimBiology provides a user-friendly ‘dragging-and-dropping’ block diagram editor to build a new model. Thanks to the powerful computing ability of Matlab, SimBiology integrates a wide range of numerical solvers for both stochastic and deterministic simulations. Another strength of SimBiology is its analysing ability which includes sensitivity analysis, parameter estimation and conservation of moieties. Last but not the least, SimBiology provides user-defined plotting function which was widely used in this research project. However SimBiology is commercial software, it costs the budgeted researchers extra expense to purchase the license for this toolbox. Also, there is no GUI for sensitivity analysis and parameters scan functions, so users should obtain the skill of programming with Matlab.

2.BIOCHAM: BIOCHAM stands for biochemical abstract machine which is a formal modeling environment for system biology. Because of its rule-based language and temporal logic based language, BIOCHAM can offer an automatically reasoning tool for querying the temporal properties of the system under all its possible behaviours. It is very useful for constructing models especially when numerical data is unavailable. BIOCHAM also provides a state-of-the-art symbolic model checker for handling the complexity of large highly non-deterministic models. Furthermore, it provides simulation results via its graphical interface. One disadvantage of BIOCHAM is that because it is initially developed under UNIX, it uses command line rather than GUI to build new models, requiring users to write scripts by hand. Another problem was that when transplanting the program from UNIX to Windows, the model checker of NuSMV does not work well. So this project used BIOCHAM in Fedora 5 rather than Windows XP.

3. COPASI: COPASI is freeware developed with collaboration of VBI and EMLR. It provides almost the same functions as SimBiology, though not quite powerful. But compared with SimBiology, it provides a friendly user interface for model analysis, such as parameter estimation, and parameter scan. But there is no parameters/species sensitivity analysis function in COPASI, and also it is not very stable in use, crashing without any responses.

To sum up, each software has its own pros and cons. A good strategy is to apply them for different purposes, for example, using SimBiology to analyze the sensitivity of the model, and using COPASI to scan the most sensitive parameters. When logical queries are needed, BIOCHAM should be the first choice. SimBiology is suitable for generating professional plots, however due to the license requirement, COPASI can be the alternative choice to to run simulations and export the results to such plotting software as SigmaPlot.

Results

System response

Fig.1 System response with 5ppb arsenic input

When the concentration of arsenic is low, like 5ppb input, the production of Urease is at a high level above 25 units while lacZ production is at a basal level less than 5 units.

Fig.2 System response with 20ppb arsenic input

When the arsenic concentration rises to higher level like 20ppb, Urease decreases to almost zero because of the repression by LambdaCI and the concentration of lacZ increases to about 10 units because the ArsD has been captured by Arsenic molecules.

Because of the different responses of the system, a significant change of pH value is obtained.

Parameter sensitivity analysis

To provide suggestions to the experimental biologists which proteins or which reaction rates should be measured, it is important to find out the relative importance of each parameter in the system. Parameter sensitivity analysis is used to identify which parameters are more critical in effecting the output of the pathway, and help to gain a deeper insight of the structure and the function of the system.

Fig.3 Sensitivity of lacZ with Respect to Model Parameters 1-16
Fig.4 Sensitivity of lacZ with Respect to Model Parameters 17-32

The most sensitive parameters affecting lacZ

Nanme Description Peak value of sensitivity Normal value
K-1 ArsD-2AS(III) dissociate rate -20.65/s
K-2 2ArsD-promoter1 dissociate rate 4 0.65/s
K3 ArsD degradation rate 90 0.05/s
K7 ArsR degradation rate 12 0.05/s
K13 LacZ degradation rate -35 0.1/s


Fig.5 Varying the Value of Parameter K-1 effect on lacZ
Fig.6 Varying the Value of Parameter K-1 effect on lacZ (3D)
Fig.7 Varying the Value of Parameter K-2 effect on lacZ


Fig.8 Varying the Value of Parameter K3 effect on lacZ
Fig.9 Varying the Value of Parameter K7 effect on lacZ
Fig.10 Varying the Value of Parameter K13 effect on lacZ
Fig.11 Sensitivity of Urease with Respect to Model Parameters 1-16
Fig.12 Sensitivity of Urease with Respect to Model Parameters 17-32

The most sensitive parameters affecting Urease

Nanme Description Peak value of sensitivity Normal value
k3 ArsD degradation rate -300.05/s
k-6 2ArsR-promoter2 dissociate rate -5 0.65/s
k7 ArsR degradation rate -120 0.05/s
K18 Urease degradation rate -350 0.1/s
V19m Urease production maxium rate 3.5 10 nMol/s
Fig.13 Varying the Value of Parameter K3 effect on Urease
Fig.14 Varying the Value of Parameter K-6 effect on Urease
Fig.15 Varying the Value of Parameter K7 effect on Urease
Fig.16 Varying the Value of Parameter K18 effect on Urease

Species sensitivity analysis

Fig.7 Sensitivity of lacZ with Respect to Model Species

The most sensitive species affecting lacZ

NameInitial concentration (nMol)
promoter1 5.0
promoter2 5.0
ArsD-2As(III) 0
ArsD 25
ArsR 25
Fig.17 Varying the Value of Species promoter1 Effect on lacZ
Fig.18 Varying the Value of Species promoter2 Effect on lacZ
Fig.19 Varying the Value of Species ArsD-2As(III) Effect on lacZ
Fig.20 Varying the Value of Species ArsD Effect on lacZ


Fig.21 Varying the Value of Species ArsR Effect on lacZ


Fig.22 Sensitivity of Urease with Respect to Model Species

The most sensitive species affecting Urease

NameInitial concentration (nMol)
LCI 4
LacI-promoter4 0.1
promoter4 25
promoter2 5
promoter1 5
Fig.23 Varying the Value of Species LCI Effect on Urease
Fig.24 Varying the Value of Species LacI-promoter4 Effect on Urease


Fig.25 Varying the Value of Species promoter4 Effect on Urease
Fig.26 Varying the Value of Species promoter2 Effect on Urease

Appendix

Appendix 1. The Matlab scripts for multi-parameter sensitivity analysis

sbioloadproject Biosensor  %change the project name to replace “Biosensor” here

m1

m1.Species

m1.Reactions

csObj = getconfigset(m1);

% change stop time to the time you want the simulation to run for in the line below

set(csObj, 'StopTime', 500);

csObj

csObj.RunTimeOptions.StatesToLog

% in line below change urease for the output you want to monitor

csObj.RunTimeOptions.StatesToLog = sbioselect... (m1, 'type', 'species', 'Where', 'Name', '==', 'Urease');

csObj.RunTimeOptions.StatesToLog

set(csObj.SolverOptions, 'SensitivityAnalysis', true);

pif = [sbioselect(m1, 'Type', 'parameter', 'Where', 'Name', '==', 'K1');... %change the name of parameter here

sbioselect(m1, 'Type', 'parameter', 'Where', 'Name', '==', 'K-1')

sbioselect(m1, 'Type', 'parameter', 'Where', 'Name', '==', 'K2')

sbioselect(m1, 'Type', 'parameter', 'Where', 'Name', '==', 'K-2')

sbioselect(m1, 'Type', 'parameter', 'Where', 'Name', '==', 'K3')

sbioselect(m1, 'Type', 'parameter', 'Where', 'Name', '==', 'V4m')

sbioselect(m1, 'Type', 'parameter', 'Where', 'Name', '==', 'K4m')

sbioselect(m1, 'Type', 'parameter', 'Where', 'Name', '==', 'K5')

sbioselect(m1, 'Type', 'parameter', 'Where', 'Name', '==', 'K-5')

sbioselect(m1, 'Type', 'parameter', 'Where', 'Name', '==', 'K6')

sbioselect(m1, 'Type', 'parameter', 'Where', 'Name', '==', 'K-6')

sbioselect(m1, 'Type', 'parameter', 'Where', 'Name', '==', 'K7')

sbioselect(m1, 'Type', 'parameter', 'Where', 'Name', '==', 'V8m')

sbioselect(m1, 'Type', 'parameter', 'Where', 'Name', '==', 'K8m')

sbioselect(m1, 'Type', 'parameter', 'Where', 'Name', '==', 'K9')

sbioselect(m1, 'Type', 'parameter', 'Where', 'Name', '==', 'K-9')];

set(csObj.SensitivityAnalysisOptions, 'ParameterInputFactors', pif);

set(csObj.SensitivityAnalysisOptions, 'Normalization', 'None');

warning('off', 'MATLAB:divideByZero');

tsObj = sbiosimulate(m1);

[T, R, snames, ifacs] = sbiogetsensmatrix(tsObj);

size(R)

R2 = squeeze(R);

figure;

plot(T,R2);

% in lines below change the labels to suit the graph you want to draw

title('Sensitivity of Urease with Respect to Model Parameters 1-16');

xlabel('Time (seconds)');

ylabel('Sensitivity of Urease');

Appendix 2. The Matlab script for Multi-species sensitivity analysis

sbioloadproject Biosensor

m1

m1.Species

m1.Reactions

csObj = getconfigset(m1);

% change stop time to the time you want the simulation to run for in the line below

set(csObj, 'StopTime', 500);

csObj

csObj.RunTimeOptions.StatesToLog

% in line below change urease for the output you want to monitor

csObj.RunTimeOptions.StatesToLog = sbioselect... (m1, 'type', 'species', 'Where', 'Name', '==', 'Urease');

csObj.RunTimeOptions.StatesToLog

set(csObj.SolverOptions, 'SensitivityAnalysis', true);

sif = [sbioselect(m1, 'Type', 'species', 'Where', 'Name', '==', 'ArsD');...

sbioselect(m1, 'Type', 'species', 'Where', 'Name', '==', 'As(III)');...

sbioselect(m1, 'Type', 'species', 'Where', 'Name', '==', 'ArsD-2As(III)');...

sbioselect(m1, 'Type', 'species', 'Where', 'Name', '==', 'promoter1');...

sbioselect(m1, 'Type', 'species', 'Where', 'Name', '==', '2ArsD-promoter1');...

sbioselect(m1, 'Type', 'species', 'Where', 'Name', '==', 'ArsR');...

sbioselect(m1, 'Type', 'species', 'Where', 'Name', '==', 'ArsR-2As(III)');...

sbioselect(m1, 'Type', 'species', 'Where', 'Name', '==', 'promoter2');...

sbioselect(m1, 'Type', 'species', 'Where', 'Name', '==', '2ArsR-promoter2');...

sbioselect(m1, 'Type', 'species', 'Where', 'Name', '==', 'LacI');...

sbioselect(m1, 'Type', 'species', 'Where', 'Name', '==', 'allolactose');...

sbioselect(m1, 'Type', 'species', 'Where', 'Name', '==', 'LacI-allolactose');...

sbioselect(m1, 'Type', 'species', 'Where', 'Name', '==', 'promoter4');...

sbioselect(m1, 'Type', 'species', 'Where', 'Name', '==', 'LacI-promoter4');...

sbioselect(m1, 'Type', 'species', 'Where', 'Name', '==', 'promoter3');...

sbioselect(m1, 'Type', 'species', 'Where', 'Name', '==', 'lacZ');...

sbioselect(m1, 'Type', 'species', 'Where', 'Name', '==', 'LCI');...

sbioselect(m1, 'Type', 'species', 'Where', 'Name', '==', 'LCI-promoter4');...

sbioselect(m1, 'Type', 'species', 'Where', 'Name', '==', 'Urease') ];

set(csObj.SensitivityAnalysisOptions, 'SpeciesInputFactors', sif);

set(csObj.SensitivityAnalysisOptions, 'Normalization', 'None');

warning('off', 'MATLAB:divideByZero');

tsObj = sbiosimulate(m1);

[T, R, snames, ifacs] = sbiogetsensmatrix(tsObj);

size(R)

R2 = squeeze(R);

figure;

plot(T,R2);

% in lines below change the labels to suit the graph you want to draw

title('Sensitivity of Urease with Respect to Model Species');

xlabel('Time (seconds)');

ylabel('Sensitivity of Urease');

Appendix 3. The Matlab lab script for parameter scan

sbioloadproject Tuning

m1

m1.Species

m1.Reactions

csObj = getconfigset(m1);

% change stop time to the time you want the simulation to run for in the line below

set(csObj, 'StopTime', 5000);

csObj

csObj.RunTimeOptions.StatesToLog

% in line below change urease for the output you want to monitor

csObj.RunTimeOptions.StatesToLog = sbioselect... (m1, 'type', 'species', 'Where', 'Name', '==', 'promoter1');

set(csObj.SolverOptions, 'SensitivityAnalysis', false);

set(csObj.SensitivityAnalysisOptions, 'Normalization', 'None');

h1 = figure;

ax1 = gca(h1);

% in next line change Vm4 to the name of the parameter you want to scan

p = sbioselect(m1, 'Type', 'parameter', 'Name', 'K2');

% in next line the first number is the lower limit and the second number the upper limit

% of your range and the last number is the number of scans in that range

s = linspace(1000, 100000, 8);

for k = s

set(p, 'Value', k);

[T,x,names] = sbiosimulate(m1);

str = sprintf( ' k = %8.3f',k);

plot(ax1,T,x(:,1));

figure(h1);

hold on;

text(T(end),x(end,1),str);

end

axis([ax1], 'square');

% Change these lines to suit your data

title(ax1, 'Varying the Value of Parameter K18 effect on Urease');

xlabel(ax1, 'Time (seconds)');

ylabel(ax1, 'Urease (nanomoles)');

Appendix 4. The Matlab Script for species scan

sbioloadproject Biosensor

m1

m1.Species

m1.Reactions

csObj = getconfigset(m1);

% change stop time to the time you want the simulation to run for in the line below

set(csObj, 'StopTime', 500);

csObj

csObj.RunTimeOptions.StatesToLog

% in line below change urease for the output you want to monitor

csObj.RunTimeOptions.StatesToLog = sbioselect... (m1, 'type', 'species', 'Where', 'Name', '==', 'Urease');

set(csObj.SolverOptions, 'SensitivityAnalysis', false);

set(csObj.SensitivityAnalysisOptions, 'Normalization', 'None');

h1 = figure;

ax1 = gca(h1);

% in next line change Vm4 to the name of the parameter you want to scan

p = sbioselect(m1, 'Type', 'species', 'Name', 'promoter1');

% in next line the first number is the lower limit and the second number the upper limit

% of your range and the last number is the number of scans in that range

s = linspace(0, 50, 8);

for spR = s

set(p, 'InitialAmount', spR);

[T,x,names] = sbiosimulate(m1);

str = sprintf( ' R = %8.3f',spR);

plot(ax1,T,x(:,1));

figure(h1);

hold on;

text(T(end),x(end,1),str);

end

axis([ax1], 'square');

% Change these lines to suit your data

title(ax1, 'Varying the Value of Species promoter1: Effect on Urease');

xlabel(ax1, 'Time (seconds)');

ylabel(ax1, 'Urease (nanomoles)');


[http://2006.igem.org/University_of_Edinburgh_2006 Main page]

Retrieved from "http://2006.igem.org/wiki/index.php/EdinburghModeling"
Personal tools
Past/present/future years