EdinburghModeling
From 2006.igem.org
(→Methodology) |
|||
| Line 102: | Line 102: | ||
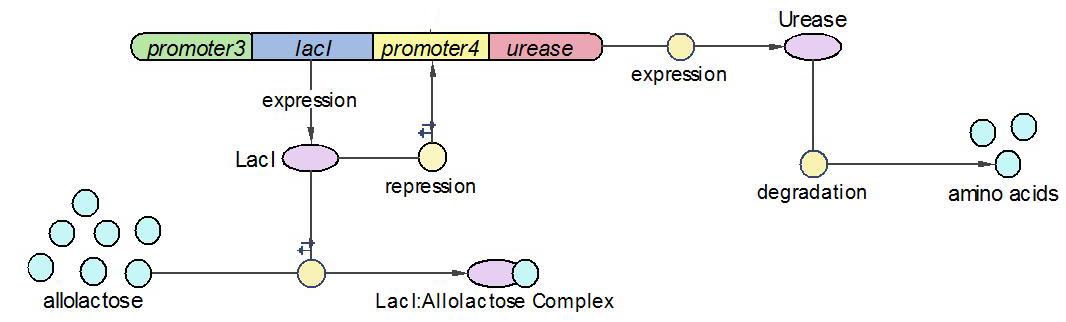
The Urease operon: | The Urease operon: | ||
| + | [[Image:EdinUrease_Operon.JPG]] | ||
===Software used=== | ===Software used=== | ||
Revision as of 12:05, 29 October 2006
Contents |
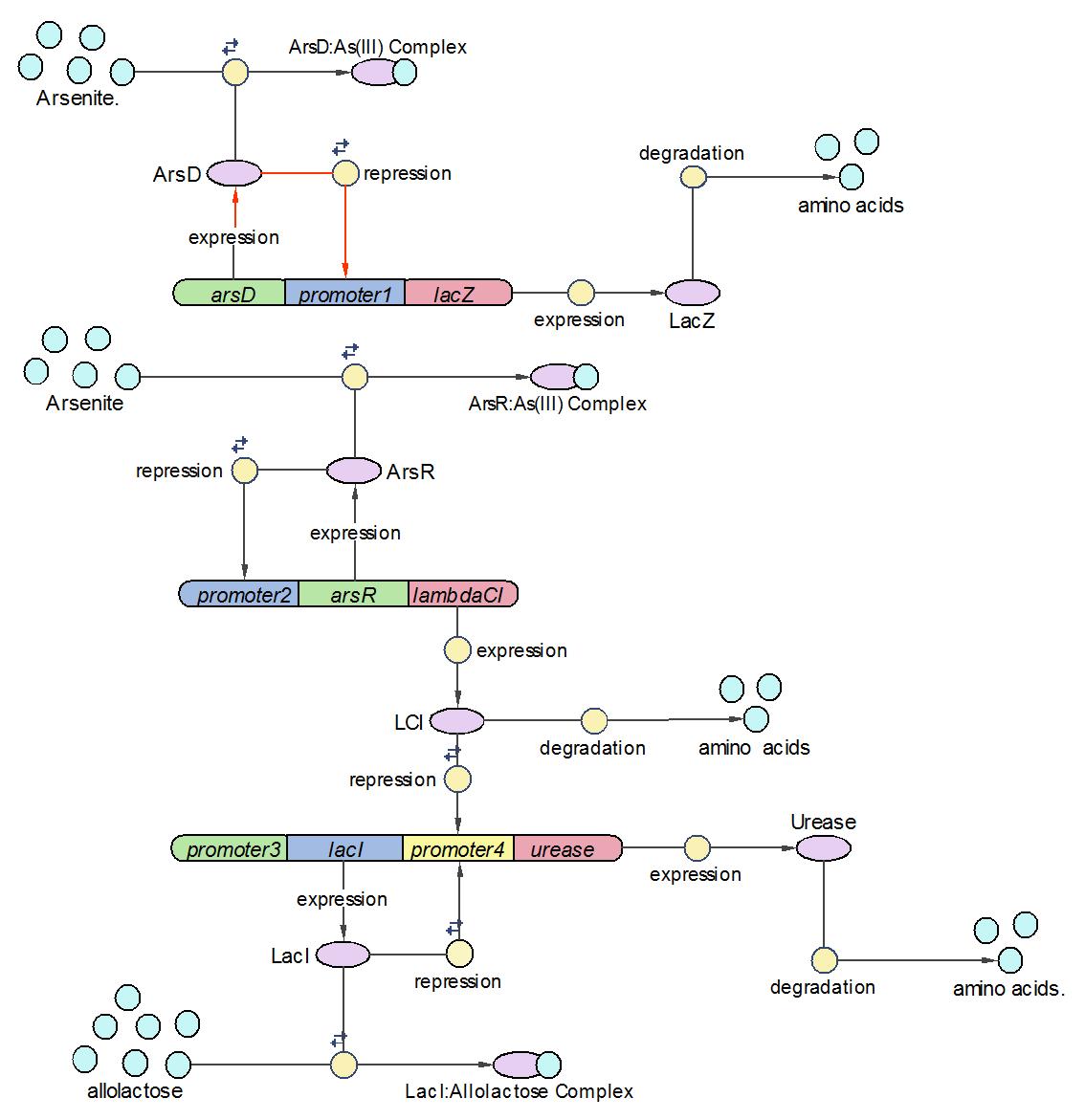
System Diagram of Arsenic Biosensor([http://2006.igem.org/Image:Modeling_the_Arsenic_Biosensor_System.pdf PDF version])
Abstract
This section reports the modeling progress of an arsenic biosensor system, which is the iGEM project accomplished in the University of Edinburgh 2006. The arsenic biosensor system sought to address the fatal water pollution problem occurring in many poor countries/areas like Bangladesh by producing a calibratable pH changes in response to a range of arsenic concentrations. A computational model which contains 3 operons, 19 reactions and 17 species has been constructed to shed light on the wet-lab experimental design. By analyzing the sensitivity of each parameter/species, we identified their relative importance in the system which gives the theoretical guide when measuring the variable in wet-lab. The next step research is to refine the model by comparing it with the biological output.
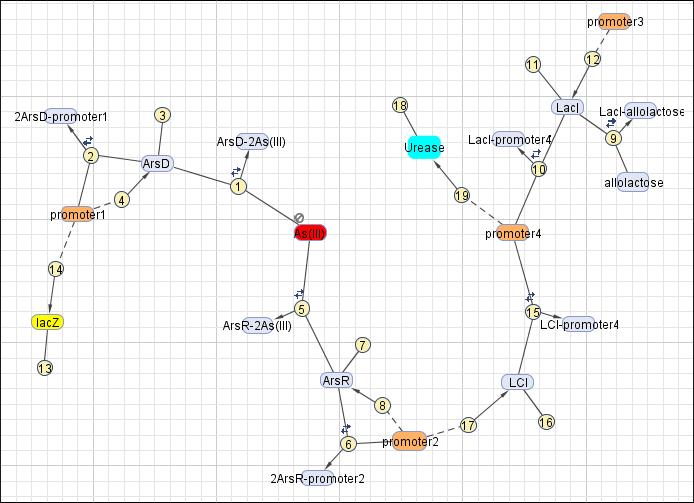
Reaction set
| No. | Name | Equation | Rate Law | Parameters |
| 1 | ArsD binding to Arsenic (III) | ArsD+2As(III)=ArsD-2As(III) | Mass Action | K1=1000 K-1=0.65 |
| 2 | ArsD binding to promoter1 | 2 ArsD+promoter1=2ArsD-promoter1 | Mass Action | K2=10000, K-2=0.65 |
| 3 | ArsD degradation | ArsD->null | Mass Action | K3=0.05 |
| 4 | ArsD production | promoter1->promoter1+ArsD | Michaelis-Menten | V4m=0.5, K4m=75 |
| 5 | ArsR binding to Arsenic (III) | ArsR+2As(III)=ArsR-2As(III) | Mass Action | K5=1000, K-5=0.65 |
| 6 | ArsR binding to promoter2 | 2ArsR+promoter2=2ArsR-promoter2 | Mass Action | K6=10000, K-6=0.65 |
| 7 | ArsR degradation | ArsR->null | Mass Action | K7=0.05 |
| 8 | ArsR production | promoter2->promoter2+ArsR | Michaelis-Menten | V8m=10, K8m=25 |
| 9 | LacI binding to allolactose | LacI+allolactose=LacI-allolactose | Mass Action | K9=10000, K-9=0.1 |
| 10 | LacI binding to promoter4 | LacI+promoter4 = LacI-promoter4 | Mass Action | K10=1000, K-10=0.5 |
| 11 | LacI degradation | LacI->null | Mass Action | K11=0.1 |
| 12 | LacI production | promoter3->promoter3+LacI | Michaelis-Menten | V12m=0.5, K12m=40 |
| 13 | lacZ degradation | lacZ->null | Mass Action | K13=0.1 |
| 14 | lacZ production | promoter1->promoter1+lacZ | Michaelis-Menten | V14m=25, K14m=10 |
| 15 | LCI binding to promoter 4 | LCI+promoter4=LCI-promoter4 | Mass Action | K15=10000, K-15=0.5 |
| 16 | LCI degradation | LCI->null | Mass Action | K16=0.1 |
| 17 | LCI production | promoter2->promoter2+LCI | Michaelis-Menten | V17m=10, K17m=25 |
| 18 | Urease degradation | Urease->null | Mass Action | K18=0.1 |
| 19 | Urease production | promoter4->promoter4+Urease | Michaelis-Menten | V19m=10, K19m=40 |
Note: The units for first, second and third order rate constants are expressed in units of second^-1, nMol^-1*second^-1 and nMol^-2*second^-1 respectively.
This reaction map is generated from the reaction set above using Simbiology Toolbox.
Initial concentration
| No. | Species | Intial Concentration (nMol) |
| 1 | ArsD | 25 |
| 2 | As(III) | 40 |
| 3 | 2ArsD-promoter1 | 25 |
| 4 | promoter1 | 5 |
| 5 | ArsR | 25 |
| 6 | 2ArsR-promoter2 | 25 |
| 7 | promoter2 | 5 |
| 8 | LCI | 4 |
| 9 | LacI | 0.1 |
| 10 | LacI-allolactose | 0.1 |
| 11 | allolactose | 1000 |
| 12 | LacI-promoter4 | 0.1 |
| 13 | promoter4 | 25 |
| 14 | LCI-promoter4 | 0.1 |
| 15 | Urease | 0.1 |
| 16 | promoter3 | 5 |
| 17 | Other species | 0 |
Ordinary Differential Equation
Methodology
The gene expression reactions are modeled using Michaelis-Menten equation while the other reactions are described in Mass-Action equations.
We divided the whole system into three operons, namely Urease operon, LambdaCI operon and LacZ operon.
Software used
In order to model the quantitative behaviour of the dynamic system, many modeling software systems have been developed in the past few years. In this project, three kinds of software systems are used for modelling. This section introduces their functions and features.
1.System biology toolbox for Matlab: SimBiology toolbox provides functions for modelling, simulating, and analysing biochemical pathways on basis of the powerful computing engine of Matlab. Aside from the conventional typing reaction equation, SimBiology provides a user-friendly ‘dragging-and-dropping’ block diagram editor to build a new model. Thanks to the powerful computing ability of Matlab, SimBiology integrates a wide range of numerical solvers for both stochastic and deterministic simulations. Another strength of SimBiology is its analysing ability which includes sensitivity analysis, parameter estimation and conservation of moieties. Last but not the least, SimBiology provides user-defined plotting function which was widely used in this research project. However SimBiology is commercial software, it costs the budgeted researchers extra expense to purchase the license for this toolbox. Also, there is no GUI for sensitivity analysis and parameters scan functions, so users should obtain the skill of programming with Matlab.
2.BIOCHAM: BIOCHAM stands for biochemical abstract machine which is a formal modeling environment for system biology. Because of its rule-based language and temporal logic based language, BIOCHAM can offer an automatically reasoning tool for querying the temporal properties of the system under all its possible behaviours. It is very useful for constructing models especially when numerical data is unavailable. BIOCHAM also provides a state-of-the-art symbolic model checker for handling the complexity of large highly non-deterministic models. Furthermore, it provides simulation results via its graphical interface. One disadvantage of BIOCHAM is that because it is initially developed under UNIX, it uses command line rather than GUI to build new models, requiring users to write scripts by hand. Another problem was that when transplanting the program from UNIX to Windows, the model checker of NuSMV does not work well. So this project used BIOCHAM in Fedora 5 rather than Windows XP.
3. COPASI: COPASI is freeware developed with collaboration of VBI and EMLR. It provides almost the same functions as SimBiology, though not quite powerful. But compared with SimBiology, it provides a friendly user interface for model analysis, such as parameter estimation, and parameter scan. But there is no parameters/species sensitivity analysis function in COPASI, and also it is not very stable in use, crashing without any responses.
To sum up, each software has its own pros and cons. A good strategy is to apply them for different purposes, for example, using SimBiology to analyze the sensitivity of the model, and using COPASI to scan the most sensitive parameters. When logical queries are needed, BIOCHAM should be the first choice. SimBiology is suitable for generating professional plots, however due to the license requirement, COPASI can be the alternative choice to to run simulations and export the results to such plotting software as SigmaPlot.
Results
System response
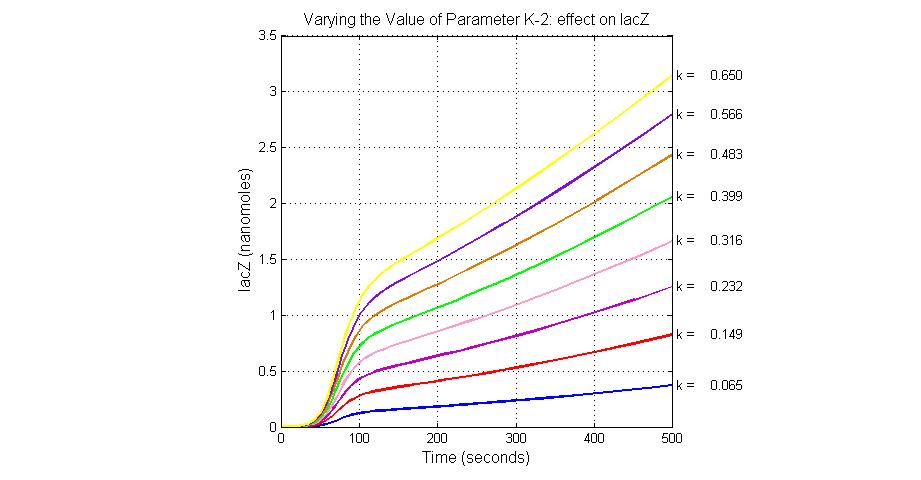
Parameter sensitivity analysis
The most sensitive parameters affecting lacZ
| Nanme | Description | Peak value of sensitivity | Normal value |
| K-1 | ArsD-2AS(III) dissociate rate | -2 | 0.65/s |
| K-2 | 2ArsD-promoter1 dissociate rate | 4 | 0.65/s |
| K3 | ArsD degradation rate | 90 | 0.05/s |
| K7 | ArsR degradation rate | 12 | 0.05/s |
| K13 | LacZ degradation rate | -35 | 0.1/s |
The most sensitive parameters affecting Urease
| Nanme | Description | Peak value of sensitivity | Normal value |
| k3 | ArsD degradation rate | -30 | 0.05/s |
| k-6 | 2ArsR-promoter2 dissociate rate | -5 | 0.65/s |
| k7 | ArsR degradation rate | -120 | 0.05/s |
| K18 | Urease degradation rate | -350 | 0.1/s |
| V19m | Urease production maxium rate | 3.5 | 10 nMol/s |
Species sensitivity analysis
The most sensitive species affecting lacZ
| Name | Initial concentration (nMol) |
| promoter1 | 5.0 |
| promoter2 | 5.0 |
| ArsD-2As(III) | 0 |
| ArsD | 25 |
| ArsR | 25 |
The most sensitive species affecting Urease
| Name | Initial concentration (nMol) |
| LCI | 4 |
| LacI-promoter4 | 0.1 |
| promoter4 | 25 |
| promoter2 | 5 |
| promoter1 | 5 |