Modeling
From 2006.igem.org
m |
|||
| Line 1: | Line 1: | ||
| - | The following model uses an Ordinary Differential Equation (ODE) based method to break down the originally proposed [[Description]] of the Thermometer into a set of ODEs. The set of equations can then used to either numerically or symbolically determine the kinetics of the system. | + | The following model uses an Ordinary Differential Equation (ODE) based method to break down the originally proposed [[Description]] of the Thermometer into a set of ODEs. The set of equations can then used to either numerically or symbolically determine the kinetics of the system. |
| - | + | ||
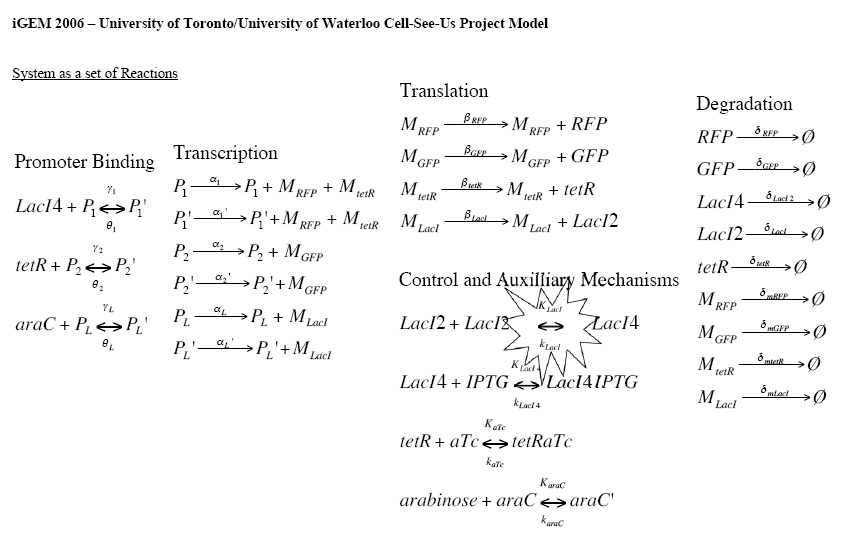
First and foremost, all interactions of the system are broken down into a set of reactions. This is shown below. | First and foremost, all interactions of the system are broken down into a set of reactions. This is shown below. | ||
| - | + | ||
| - | [[Image:System.Kinetics.jpg|650px]] | + | [[Image:System.Kinetics.jpg|650px]] |
| + | |||
The name and notation conventions are as follows: | The name and notation conventions are as follows: | ||
| - | < | + | * P<sub>subscript</sub> - Promoter |
| - | < | + | * M<sub>subscript</sub> - mRNA molecules |
| - | < | + | * γ<sub>subscript</sub> - substrate binding rate to promoter |
| - | < | + | * θ<sub>subscript</sub> - substrate unbinding rate from promoter |
| - | < | + | * α<sub>subscript</sub> - transcription rate |
| - | < | + | * β<sub>subscript</sub> - translation rate |
| - | < | + | * δ<sub>subscript</sub> - degradation rate |
| - | < | + | * K<sub>subscript</sub> - binding rate for control mechanism |
| - | < | + | * k<sub>subscript</sub> - unbinding rate for control mechanisms |
| - | < | + | |
| - | + | From here, the Law of Mass Action is used to describe the rate of change of each molecule (and gene) with respect to time. Since this is a closed system, the rates of change for each molecule are summated to produce the following set of equations. | |
| - | + | ||
| - | From here, the Law of Mass Action is used to describe the rate of change of each molecule (and gene) with respect to time. Since this is a closed system, the rates of change for each molecule are summated to produce the following set of equations. | + | [[Image:System.Diff.Equations.jpg|650px]] |
| - | [[Image:System.Diff.Equations.jpg|650px]] | + | |
| - | A PDF is available here [[Media:IGEM_2006_-_Temperature_Sensor_Model_DRAFT_4.pdf]] | + | A PDF is available here [[Media:IGEM_2006_-_Temperature_Sensor_Model_DRAFT_4.pdf]]. |
| - | + | ||
| + | |||
| + | --[[User:Scwleung|Scwleung]] 21:48, 1 November 2006 (EST) | ||
Revision as of 04:15, 2 November 2006
The following model uses an Ordinary Differential Equation (ODE) based method to break down the originally proposed Description of the Thermometer into a set of ODEs. The set of equations can then used to either numerically or symbolically determine the kinetics of the system.
First and foremost, all interactions of the system are broken down into a set of reactions. This is shown below.
The name and notation conventions are as follows:
- Psubscript - Promoter
- Msubscript - mRNA molecules
- γsubscript - substrate binding rate to promoter
- θsubscript - substrate unbinding rate from promoter
- αsubscript - transcription rate
- βsubscript - translation rate
- δsubscript - degradation rate
- Ksubscript - binding rate for control mechanism
- ksubscript - unbinding rate for control mechanisms
From here, the Law of Mass Action is used to describe the rate of change of each molecule (and gene) with respect to time. Since this is a closed system, the rates of change for each molecule are summated to produce the following set of equations.
A PDF is available here Media:IGEM_2006_-_Temperature_Sensor_Model_DRAFT_4.pdf.
--Scwleung 21:48, 1 November 2006 (EST)