Davidson 2006
From 2006.igem.org
(Difference between revisions)
(→<div id="overview">Solving the Pancake Problem with an E. coli Computer</div>) |
|||
| Line 6: | Line 6: | ||
---- | ---- | ||
| - | + | <big>'''<div id="overview">Solving the Pancake Problem with an E. coli Computer</div>'''</big> | |
| Line 15: | Line 15: | ||
Our project integrates math and biology using the [http://en.wikipedia.org/wiki/Pancake_sorting pancake problem], a puzzle in which a scrambled series of units (or stack of pancakes) must be shuffled into the correct order. You can try solving [http://www.cut-the-knot.org/SimpleGames/Flipper.shtml a version of the pancake problem] yourself. | Our project integrates math and biology using the [http://en.wikipedia.org/wiki/Pancake_sorting pancake problem], a puzzle in which a scrambled series of units (or stack of pancakes) must be shuffled into the correct order. You can try solving [http://www.cut-the-knot.org/SimpleGames/Flipper.shtml a version of the pancake problem] yourself. | ||
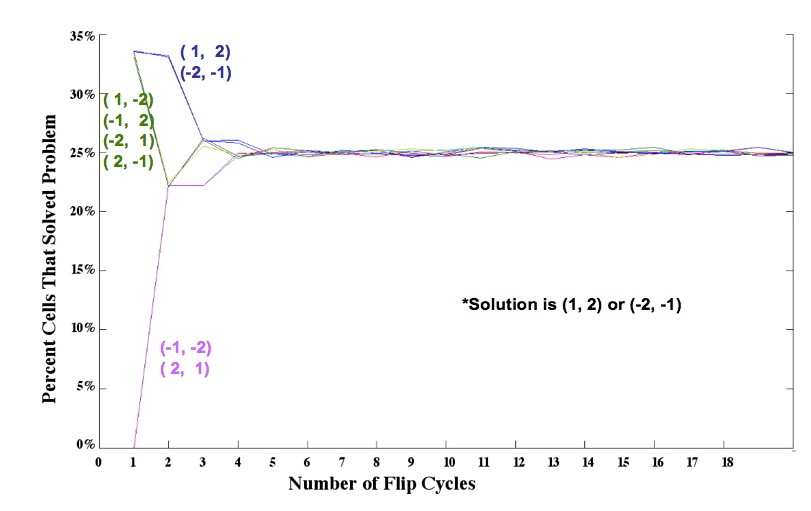
| - | In the burnt pancake problem, each pancake is given an orientation by burning one side. Figure 1 shows a scrambled stack of burnt pancakes. Every unit, or pancake, must be placed in the proper order (largest on bottom, smallest on top) ''and'' in the proper orientation (burnt side down, golden side up). Pancakes are sorted with two spatulas. One spatula is used to lift zero or more pancakes off the top of the stack, while the second spatula flips a stack of one or more of the remaining pancakes. The pancakes lifted by the first spatula are then returned to the top of the stack. You can watch a movie of the stack in Figure 1 being sorted. Trial and error is one approach to solving the problem, but how could one compute the quickest solution? | + | {| |
| + | |- valign="top" | ||
| + | |[[Image:four_pancakes.jpg|thumb|250px|left|Simulation results for two pancakes, useful for calibrating kinetics of pancake flipping. ]]In the burnt pancake problem, each pancake is given an orientation by burning one side. Figure 1 shows a scrambled stack of burnt pancakes. Every unit, or pancake, must be placed in the proper order (largest on bottom, smallest on top) ''and'' in the proper orientation (burnt side down, golden side up). Pancakes are sorted with two spatulas. One spatula is used to lift zero or more pancakes off the top of the stack, while the second spatula flips a stack of one or more of the remaining pancakes. The pancakes lifted by the first spatula are then returned to the top of the stack. You can watch a movie of the stack in Figure 1 being sorted. Trial and error is one approach to solving the problem, but how could one compute the quickest solution? | ||
Our approach is to | Our approach is to | ||
Revision as of 04:26, 27 October 2006
 Project Overview [http://partsregistry.org/cgi/partsdb/pgroup.cgi?pgroup=iGEM2006partsregistry.org/cgi/partsdb/pgroup.cgi?pgroup=iGEM2006&group=Davidson Davidson Parts] Team Members Tools and Resources Check out our [http://www.bio.davidson.edu/courses/synthetic/photos/FlapJack_HotCakes.html Official Team Photo] |  |
Solving the Pancake Problem with an E. coli Computer
Our goal is to mathematically model and genetically engineer a biological system that can compute solutions to a puzzle called the burnt pancake problem. Our work was done in collaboration with the [http://2006.igem.org/wiki/index.php/Missouri_Western_State_University_2006 Missouri Western iGEM Team] and an undergraduate research fellow from [http://www.hamptonu.edu/ Hampton University].
The Burnt Pancake Problem
Our project integrates math and biology using the [http://en.wikipedia.org/wiki/Pancake_sorting pancake problem], a puzzle in which a scrambled series of units (or stack of pancakes) must be shuffled into the correct order. You can try solving [http://www.cut-the-knot.org/SimpleGames/Flipper.shtml a version of the pancake problem] yourself.
 Our approach is to model the problem by representing a pancake stack mathematically and biologically. A stack of pancakes can be represented by a series of integers in a certain order (ie. 1, 2, 3 vs. 3, 2, 1) where orientation is represented by a positive or negative value (1 vs. -1). Similarly, a series of DNA segments has a certain order (ie. promoter, coding region 1, coding region 2) and each unit has two possible orientations (plus strand vs. minus strand).
Building the Biological System
TEAM MEMBERS
Faculty
TOOLS AND RESOURCES
White Board Biology Tools (Wet Bench)
Math Tools
Bio-Math Tools
Assembly Plans Progress |
