Modeling

From 2006.igem.org

The following model uses an Ordinary Differential Equation (ODE) based method to break down the originally proposed Description of the Thermometer into a set of ODEs. The set of equations can then used to either numerically or symbolically determine the kinetics of the system.

First and foremost, all interactions of the system are broken down into a set of reactions. This is shown below.


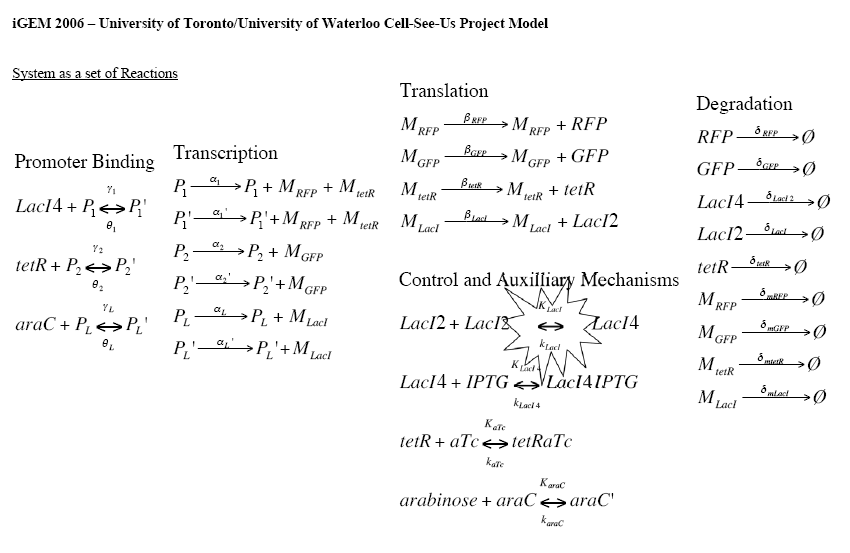
The name and notation conventions are as follows:

• P_subscript - Promoter
• M_subscript - mRNA molecules
• gamma_subscript - substrate binding rate to promoter
• theta_subscript - substrate unbinding rate from promoter
• alpha_subscript - transcription rate
• beta_subscript - translation rate
• delta_subscript - degradation rate
• K_subscript - binding rate for control mechanism
• k_subscript - unbinding rate for control mechanisms

From here, the Law of Mass Action is used to describe the rate of change of each molecule (and gene) with respect to time. Since this is a closed system, the rates of change for each molecule are summated to produce the following set of equations.


A PDF is available here Media:IGEM_2006_-_Temperature_Sensor_Model_DRAFT_4.pdf .

--Scwleung 21:48, 1 November 2006 (EST)