Mathematical Modeling

From 2006.igem.org

Contents 1 Sensitivity Analysis 1.1 Intro 1.2 Monte Carlo Method 2 Results 3 Results from cloning 4 Parameter Ranges 5 Which two Zincfingers should have the same affinity? 6 Deriving a model 6.1 General approach 6.2 Application to the counter circuit 6.3 Possible model improvements 7 Matlab Code 7.1 Zipped Matlab Code 7.2 Simulation for people who don't know how to handle Matlab 7.3 How does the simulation work? 7.3.1 maincounter.m 7.3.2 ode_counter.m 7.3.3 act.m 7.3.4 rep.m 7.3.5 input_signal.m 7.3.6 jury.m 7.3.7 test_oscillation.m 7.4 What if I want to automatically test several sets of parameters? 7.4.1 K_kd_iterate.m 7.4.2 maincounter_iterate.m

Sensitivity Analysis

Intro

The goal of sensitivity analysis is to find out to which parameters our model is sensitive. When some parameters are changed slightly, the system can respond anywhere between strongly and weakly. If it reacts strongly, i.e. the output of the system changes drastically, then the system is very sensitive to that parameter. If the system only changes its output slightly (or not at all) when a certain parameter is changed, the system is said to be insensitive to that parameter.

It goes without saying that especially the sensitive parameters need to be taken care of, as the setting of the insensitive parameters doesn't change the output of the system much. Based on the sensitive parameters it can be decided which parameters should be tested.

Monte Carlo Method

One method to find the sensitive parameters is the Monte Carlo Method. It works as follows:

1. The nominal parameters for the observed output f_obs are chosen. In our case, these parameters should be chosen such that the oscillation works correctly. The observed output serves as a reference for all the outputs that generated with varied input parameters.
2. The observed output is calculated, which means that the differential equations need to be solved. In our case, the observed output is the concentration of zincfinger 4 (because ZF4 oscillates best for that set of nominal parameters).
3. The parameters whose sensitivity is to be compared are chosen. In our case, only two parameters at a time are compared (because the computational effort increases exponentially with the number of parameters that are to be compared).
4. For both chosen parameters, generatie a series of independet random numbers that are uniformly distributed within the range of the respective parameter.
5. For each set of random parameter values (i.e. one random value of parameter 1 and one random value from parameter 2, for every possible combination of the random values) solve the differential equations to get the perturbed output f_per.
6. For each perturbed output calculate the corresponding objective function as follows:

<math>f_{obj}(k) = \sum_{i=1}^q (f_{obs}(i) - f_{per}(i,k))^2</math> (why the hell doesn't this *f--* math thing work ?!?), which is the sum of square errors between the initial observed and the perturbed error.

1. (Here it should continue with 7.) Set the acceptance criterion as the average of the objective function.
2. A set of parameters is acceptable if it is greater than the criterion, else it is unacceptable.
3. For both parameters, calculate the frequency distribution, i.e. count for every random number (from step 3) the number of objective functions that are acceptable or unacceptable, respectively (for example: for each random of parameter 1 there is one objective function for every random value of parameter 2).
4. For both parameters, calculate the accumulated frequency distributions for the acceptable und the unacceptable cases (i.e. add them together incrementally).
5. To measure the sensitivity of the parameters, calculate the correlation coefficient between the cumulative distributions for the acceptable and the unacceptable cases.
6. Compare the correlation coefficients of the two parameters. The parameter with the lower correlation coefficient is more sensitive than the other.

Results

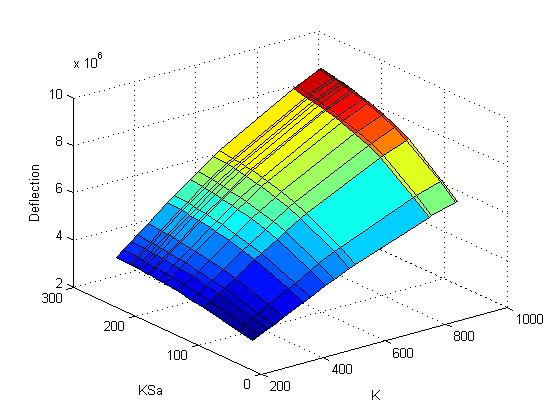
In the following picture it can be seen that a change in K (affinity of the zincfingers) leads to a bigger deflection in the objective function than a change in KSa (affinity of the input S). The calculated correlation coefficients for that picture are 0.9931 for KSa and 0.6464 for K. Hence, K is more sensitive than KSa and therefore more important.

The nominal parameters were:

n  = 2;  %cooperativity of the zincfingers
nSa  = 2; %cooperativity of S (as an activator)
nSr  = 2; %cooperativity of S (as a repressor)
K  = 100; %affinity
KSa  = 100; 
KSr  = 3*KSa; %Pr is stronger than Prm; see below
k  = 700; %maximum expression rate
kd  = 1.5; %degradation rate
period = 30;
SA = 300; %amplitude of S

	Parameter 1	n	nS	K	KS	k	kd	SA
Parameter 2	-	-	-	-	-	-	-
n	-	-	1.235723393	0.744871378	1.50413952	1.206867401	0.737546517	1.381797554
nS	-		-	0.611841593	0.876819023	0.702149543	0.637910859	0.913504404
K	-			-	1.32273205	0.747314651	0.747131882
KS	-				-
k	-					-
kd	-						-

Results from cloning

• The basal activity of Pr and Prm were compared. It seems that Pr is about 3-6 times stronger than Prm. Thus, the value of KSr is 3-6 times higher than KSa (which are the affinities for the repressing and the activating modes of S, respectively).

Parameter Ranges

It seems like there is quite a bit of confusion about what equations to use and what the ranges of the parameters are. Below is a table of how I see it at the moment.

	rep = 1/(1+(r/K)^n)	rep = 1/(1+K*r^n)
k	100 - 1000 min^-1	100 - 1000 min^-1
K	10 - 1000 nM	für n=1: 0.1 - 0.001 nM
kd	0.1 - 10 nM * min^-1	0.1 - 10 nM*min^-1

Where k is the synthesis coefficient,

K is the Affinity,

kd is the degradation coefficient

Which two Zincfingers should have the same affinity?

At the meeting yesterday, the question came up whether some zincfingers need to have the same affinity. Because as it is, we don't have four zincfingers with the same affinity. So I did some quick modeling, assuming that two ZFs have an affinity of 3 nmol and the other two an affinity of 30 nmol. As it turns out, the only constellation that works is if ZF1 and ZF3 have an affinity of 30 and ZF2 and ZF4 an affinity of 3:

Deriving a model

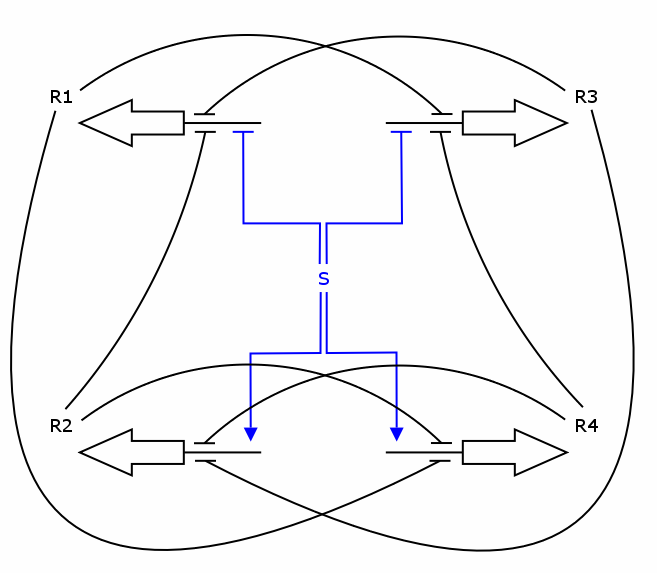
Recall the counter architecture:

We want to describe the concentrations of R1 - R4 over time given the input signal S. We will set up a deterministic model using ordinary differential equations (ODEs), as this approach is commonly used in modelling gene networks.

General approach

We have to formulate for each gene product an ODE describing its rate of change. This rate is comprised of a term characterizing the synthesis rate and one characterizing the degradation rate.

We assume that the degradation rate of a protein depends linearly on its concentration, i.e.

deg(p) = -k_deg*p

where k_deg is a degradation constant.

As for the synthesis rate we have to consider that gene expression is controlled by regulatory proteins, either in an activating or a repressing manner.

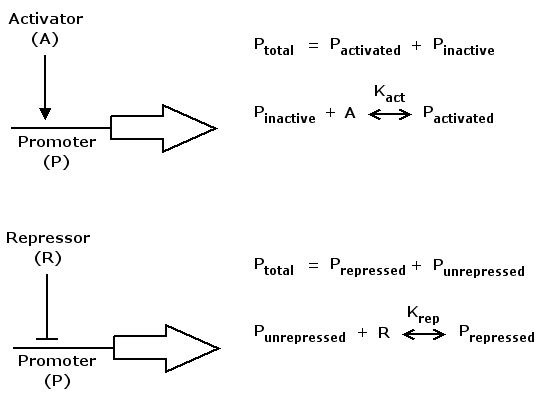
Mathematically, activation kann be formulated in the following way

act(A) = (K_act*A)^n / (1+(K_act*A)^n)

where A is a regulatory protein activating gene expression, K_act is a constant characterizing promoter-activator affinity (see figure above) and n describes the cooperativity of the activator. act(A) is in the range of [0 .. 1] and increases monotonically with increasing A.

Repression can be formulated accordingly

rep(R) = 1 / (1+(K_rep*R)^n)

where R is a regulatory protein repressing gene expression, K_rep and n are the equivalents of K_act and n in the activation case. rep(R) is in the range of [0 .. 1] and decreases monotonically with increasing R.

To get a synthesis rate we can multiply both act() and rep() with a kinetic constant k that describes the maximum synthesis rate. So on the one hand act() and rep() denote the synthesis rate relative to the maximum rate. On the other hand we can interpret them as probabilities. That is, the probability of any RNA polymerase molecule binding to the respective promoter and starting the protein synthesis process.

The total rate of change is then obtained by adding together the degradation and synthesis rates.

Application to the counter circuit

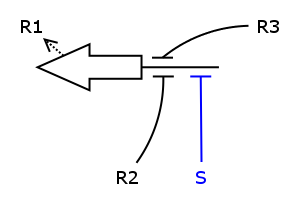
We now have all the building blocks we need to construct the ODEs for R1 - R4. Let's have a closer look at one of those Rs, say R1.

As one can see, the production of R1 depends on S, R2 and R3, i.e. S activates the production and R2/R3 repress it. We assume the individual repressors and activators affect the synthesis of R1 independently from each other, which means we can use the expressions for activation and repression that we have already formulated for each regulator separately. As we stated above the values of act() and rep() can be interpreted as probabilities. So what we need to model is the probability of three independent events coinciding. As we know from probability theory we obtain the desired probability by multiplying the individual event probabilities. Gluing everything together we get

dR1/dt = k_syn_R1 * act(S) * rep(R2) * rep(R3)  -  k_deg_R1 * R1
         \_________________ _________________/  \_______ _______/
                           V                            V
                    synthesis rate               degradation rate

Similarly we construct the other equations

 dR2/dt = k_syn_R2 * rep(S) * rep(R3) * rep(R4)  -  k_deg_R2 * R2
 dR3/dt = k_syn_R3 * act(S) * rep(R1) * rep(R4)  -  k_deg_R3 * R3
 dR4/dt = k_syn_R4 * rep(S) * rep(R1) * rep(R2)  -  k_deg_R4 * R4

Possible model improvements

Since the biological implementation of the circuit is split up into the Input Device and 4 overlapping NOR Devices, a more detailed/sophisticated model would probably give a better approximation to the actual circuit.

Matlab Code

Zipped Matlab Code

For those who want to try out the Matlab code, please use the zipped version and not the *.m files on the wiki (because those have been adapted to fit into the wiki and hence contain mistakes).

[http://www.tik.ee.ethz.ch/%7ebarkows/counter.zip Matlab gezippt]

Simulation for people who don't know how to handle Matlab

1. If you don't have Matlab on your computer, install it (unfortunately, it's payware).
2. Save all the *.m files (Matlab-files) from the zipped Matlab Code to your computer.
3. Open Matlab.
4. Set the 'Current Directory' path (above the Matlab terminal) to the folder where you stored the *.m files.
5. In the file 'maincounter.m', set the parameters you want to simulate.
6. In the Matlab terminal, type 'maincounter' in the command line.
7. The computation takes about 2 seconds. Matlab then draws a plot where you can see the impact your chosen parameters have on the concentractions.

How does the simulation work?

maincounter.m

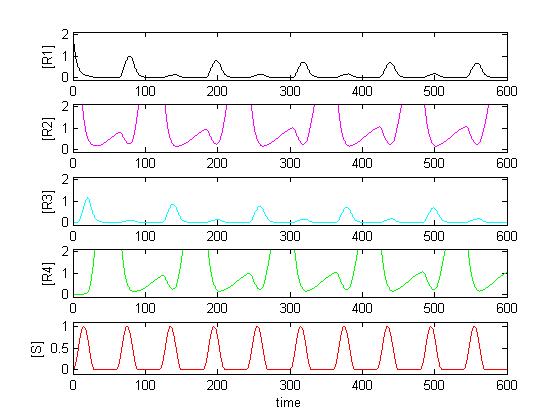
The main program is maincounter.m. First, the parameters are defined. Secondly, Matlab solves the differential equation (which are defined in ode_counter.m) using ode15s. Thirdly, a plot containing the input signal and all four concentrations is created. Last, Matlab calls the function jury.m which tells us whether the concentrations oscillates (which of course is what we want).

ode_counter.m

Here, the differential equations are defined. These are in words: The variation of a protein's concentration is equal to the product of activation and repression (because zincfingers act as roadblocks) minus a fixed part of the concentration itself (degradation).

act.m

Here, the equation we use for activation is defined.

rep.m

Here, the equation we use for reprimation is defined.

input_signal.m

The input signal is defined. You can choose between different input signals. The default input signal is a sinusoidal oscillation with 'breaks' (sections where the input remains zero between the sinusoidal peaks).

jury.m

Here, the function test_oscillation.m is called for every one of the four concentrations. jury.m returns one if any of the test_oscillation.m calls returned one (i.e. it suffices if one concentration is properly oscillating, because we can then choose that one to be the 'counting' concentration).

test_oscillation.m

Although the code looks quite complicating, what it does is pretty simple: It looks if the peaks (which of course have to occur with half the frequency of the input signal) are at least twice as big than the biggest point between the peaks (caused by noise).

What if I want to automatically test several sets of parameters?

You have set all parameters and done a simulation run. The result is negative (i.e. the concentrations don't oscillate correctly). You think you know which parameter you have to change to achieve a positive result, but you don't know how much you need to change it. There are two ways of finding that out:

1. Change the parameter of interest by hand and do a simulation run. Look at the plot, and write down if that specific value works. Change the parameter again, do another simulation run, etc. If you want to test a large range of values (e.g. K from 1 to 1000 with stepsize 5), this approach is way too onerous (200 iterations). Instead, try the following:
2. Use the function K_kd_iterate.m.

K_kd_iterate.m

Until now, only an iteration of K (zincfinger affinity) and kd (zincfinger degradation rate) has been implemented.

It works as follows: Create a vector with the values to be tested (of K and kd, respectively). Note that a higher K means a higher affinity (see the repression equation rep.m for details).

K_kd_iterate.m calls maincounter_iterate.m for every possible combination of K and kd. Be careful not to chose too large vectors. If you try 20 values for K and 20 values for kd, the computation takes a little more than ten (!) minutes.

maincounter_iterate.m

maincounter_iterate.m is the same as maincounter.m, only adapted to be used by K_kd_iterate.m (i.e. you can't set the parameters K and kd anymore).