Synthetic Counter (iGem2005 ETH Zurich)
From 2006.igem.org
Christophe (Talk | contribs) (→Input Module) |
(→Simulation: (swap activation/repression by S)) |
||
| (54 intermediate revisions not shown) | |||
| Line 1: | Line 1: | ||
| - | '''Abstract.''' We report here the design and implementation ''in vivo'' of a gene circuit that can count up to 4. In essence, | + | '''Abstract.''' We report here the design and implementation ''in vivo'' of a gene circuit that can count up to 4. In essence, the counteruses two toggle switches, each storing 1 bit, to keep track of the 4 states. The design of the counter is highly modular, with the hope that it can be included as a unit in larger circuits, and also combined with further counter instances to keep track of a much larger number of states, up to (2^(n+1)) with n units. To facilitate further developments and integration to other projects, the counter is available in form of BioBricks. Among many exciting applications, the availability of a counter enables the execution of sequential instructions, and paves the way for the execution of artifical programs inside living cells. |
=Introduction= | =Introduction= | ||
| - | The past few years have seen the emergence of the field of synthetic biology, in which functional units are designed and built into cells to generate a particular behaviour, and ultimately to better understand Life's mechanisms. Previous efforts include the creation of gene circuits that generate oscillating behaviour ([[Elowitz00]]), toggle switch functionality ([[Atkinson03]]), artificial cell-cell communication ([[Bulter04]]) or pattern-forming behaviour ([[Basu2005]]). The present document describes the design and realization of a gene circuit that counts to 4. | + | The past few years have seen the emergence of the field of synthetic biology, in which functional units are designed and built into living cells to generate a particular behaviour, and ultimately to better understand Life's mechanisms. Previous efforts include the creation of gene circuits that generate oscillating behaviour ([[Elowitz00]]), toggle switch functionality ([[Atkinson03]]), artificial cell-cell communication ([[Bulter04]]) or pattern-forming behaviour ([[Basu2005]]). The present document describes the design and realization of a gene circuit that counts to 4. |
=Design of the Counter= | =Design of the Counter= | ||
| Line 22: | Line 22: | ||
[[Image:inputPops.png]] | [[Image:inputPops.png]] | ||
| + | |||
| + | === Biological Implementation === | ||
To achieve such behaviour, we use the λ-system, with IPTG as inductor. It is relatively easy to handle/debug, and does not restrict the module from being extended to work with other types of inputs. More importantly, it is already available as a BioBrick (Registry package 7.05) in its unidirectional flavour (In nature, the λ-system is bidirectional, with Pr on one DNA strand and Prm on the other, overlapping). The following picture shows the gene circuit of the input module in details: | To achieve such behaviour, we use the λ-system, with IPTG as inductor. It is relatively easy to handle/debug, and does not restrict the module from being extended to work with other types of inputs. More importantly, it is already available as a BioBrick (Registry package 7.05) in its unidirectional flavour (In nature, the λ-system is bidirectional, with Pr on one DNA strand and Prm on the other, overlapping). The following picture shows the gene circuit of the input module in details: | ||
| - | [[Image:Lambda-Sys in INPUT-moduleSmall.jpg|Modified Lambda-system in INPUT-module: unidirectional, no OR3]] | + | [[Image:Lambda-Sys in INPUT-moduleSmall.jpg|450px|Modified Lambda-system in INPUT-module: unidirectional, no OR3]] |
| - | cI is a dimer and regulates the activity of the two promoter regions, Pr and Prm, on the λ-system. Pr is constitutively active and is repressed when cI binds to the two operator regions it overlaps with (OR1, OR2). Conversly, Prm has low basal activity, and is activated by cI. | + | cI is a dimer and regulates the activity of the two promoter regions, Pr and Prm, on the λ-system. Pr is constitutively active and is repressed when cI binds to the two operator regions it overlaps with (OR1, OR2). Conversly, Prm has low basal activity, and is activated by cI. Since the two promoters are regulated by the same protein-operator interactions, repression and activation is expected to be symmetrical (a necessary condition, see results from simulation below). For more details, please consult the page [[Input-module]]. |
| - | + | ||
| - | Since the two promoters are regulated by the same protein-operator interactions, repression and activation | + | |
==NOR Module== | ==NOR Module== | ||
| + | |||
| + | The "NOR" module uses two inputs to sequencially switch through its outputs 1, 2, 3 and 4. To achieve such behaviour, we use four interconnected "NOR" gates. In essence, a NOR gate is a component that has two inputs and one output, where the output is only high if '''none''' of the input is high. Concretly, a NOR gate can be implemented through a promoter with high basal activity that is repressed by two effectors. In the particular case, our NOR gates have ''three'' inputs (or effectors), none of which must be active for the gene to be expressed. | ||
| + | |||
| + | The following diagram (which should be redrawn using better tools than ASCII art) shows how the four NOR gates are interconnected: | ||
| + | |||
| + | R3 R2 R4 R1 R4 R3 R1 R2 | ||
| + | | | | | | | | | | ||
| + | /|____ | | | | ____|\ /|____ | | | | ____|\ | ||
| + | ___/ R1 |_=_=___ ___=_=_| R3 \___ ___/ R2 |_=_=___ ___=_=_| R4 \___ | ||
| + | \ ____| = = |____ / \ ____| = = |____ / | ||
| + | \| | | |/ \| | | |/ | ||
| + | \ / \ / | ||
| + | \ / \ / | ||
| + | |||
| + | input 2 input 1 | ||
| + | |||
| + | The design is highly symmetrical. We have 4 genes producing 4 repressor proteins R1, R2, R3 and R4. The production of each protein uses a constitutive promoter, which is down-regulated by 3 specific repressors, the two "following" repressors as well as either input 1 (for R2 and R4) or input 2 (for R1 and R3). By design of the input module, input 1 and input 2 have opposite activity, meaning that either R1/R3 or R2/R4 is active. Furthermore, since R1/R3 (respectively R2/R4) are repressing each other, only one of the two is active. Therefore, in a stable situation, only 1 of the 4 repressor proteins is expressed. | ||
| + | |||
| + | Let us assume that R1 is being expressed. Input 2 must then be low, and therefore input 1 high. This situation is stable and remains until there is a change in the inputs. Now, if input 1 decreases, and input 2 increases, the expression of R1 will come to a halt. Since input 1 is now low, either R2 or R4 will be expressed. At this stage, R1 is still present in relatively high concentration and by repressing R4, it tips the balance in favor of R2, leading to a new stable state in which only R2 is expressed. | ||
| + | |||
| + | Note that electrical engineers call such a device a "J-K flip flop". It can also be seen as a combination of two toggle switches ([[Atkinson03]]), each being able to store one bit. | ||
| + | |||
| + | === Biological Implementation === | ||
| + | |||
| + | We use zink-fingers proteins (ZFP) as repressors. This class of proteins bind to specific base pairs on the DNA. Many protein-DNA interaction for ZF domains and triplet of base pairs have been described, therefore making it possible to to construct artificial transcription factors by combining ZF domains in a modular fashion. The idea is to use a ZFP as a repressor by putting a binding site for a ZFP upstream of the coding region and thereby preventing RNA polymerase to transcribe the gene. | ||
=Simulation= | =Simulation= | ||
| + | |||
| + | The simulation was performed through a deterministic model using ordinary differential equations (ODEs), as this approach is commonly used in modelling gene networks. Recall the counter architecture: | ||
| + | |||
| + | [[Image:ModelCounterArch.png|350px]] | ||
| + | |||
| + | (S is here the input of the counter. Note that the work of the input module is symbolized here by the dual effect of S, once as an activator and once as a repressor. In reality and as described in the section above, the input signal is converted to 2 opposite signals, both of them acting as repressors, alternatively.) | ||
| + | |||
| + | The 4 corresponding differential equations are: | ||
| + | |||
| + | dR1/dt = k_syn_R1 * rep(S) * rep(R2) * rep(R3) - k_deg_R1 * R1 | ||
| + | dR2/dt = k_syn_R2 * act(S) * rep(R3) * rep(R4) - k_deg_R2 * R2 | ||
| + | dR3/dt = k_syn_R3 * rep(S) * rep(R1) * rep(R4) - k_deg_R3 * R3 | ||
| + | dR4/dt = k_syn_R4 * act(S) * rep(R1) * rep(R2) - k_deg_R4 * R4 | ||
| + | \_________________ _________________/ \_______ _______/ | ||
| + | V V | ||
| + | synthesis rate degradation rate | ||
| + | |||
| + | where act(A) = (K_act*A)^n / (1+(K_act*A)^n) | ||
| + | and rep(R) = 1 / (1+(K_rep*R)^n) | ||
| + | |||
| + | K are affinity constants, while k are kinetic constants. | ||
| + | |||
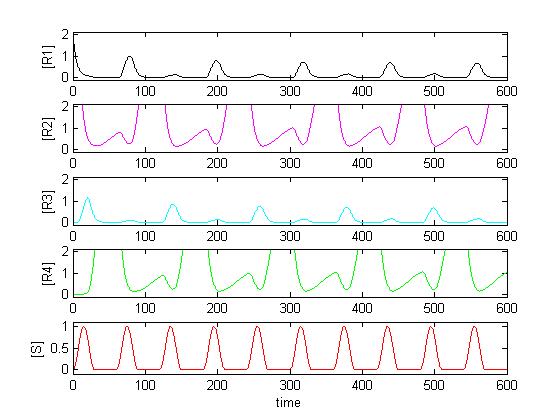
| + | Since R1 to R4 all use the same constitutive promoter, all kinetic constants k_syn_R* have the same value. Solving the system in Matlab using reasonable affinity and kinetic constants, the result can look as follows: | ||
| + | |||
| + | [[Image:K13 30 K24 3.jpg]] | ||
| + | |||
| + | As expected, [R3] follows every second peak of [S]. | ||
| + | |||
| + | By exploring the parameter space and performing [[Modeling_and_overall_design#Sensitivity_Analysis|Sensitivity Analysis]], the following conclusions could be drawn: | ||
| + | * Changes in the affinity of the zink fingers affect the system more strongly than changes in the affinity of the input S. | ||
| + | * The affinity constants R1..R4 should be as symmetrical as possible, in particular the couples R1,R3 and R2,R4. A difference in the affinity constant up to an order of magnitude appears tolerable. | ||
| + | * ... | ||
| + | More details of the simulation work are reported on the page [[Modeling_and_overall_design]]. | ||
| + | |||
=Implementation= | =Implementation= | ||
=Results and Discussion= | =Results and Discussion= | ||
| - | =Applications and | + | =Applications and Perspectives= |
| + | |||
| + | |||
| + | =Abstract for Colloquium Calzone= | ||
| + | The past few years have seen the emergence of the field of synthetic biology, in which functional units are designed and built into living cells to generate a particular behaviour, and ultimately to better understand Life's mechanisms. Previous efforts include the creation of gene circuits that generate oscillating behaviour, toggle switch functionality, artificial cell-cell communication or pattern-forming behaviour. This summer, a team of students from ETH worked on the design and implementation in-vivo of a gene circuit that counts up to 4, in the context of the international competition "iGEM", organized by MIT. Among many exciting applications, the availability of a counter enables the execution of sequential instructions, and paves the way for the execution of artifical programs inside living cells. | ||
Latest revision as of 18:54, 27 October 2005
Abstract. We report here the design and implementation in vivo of a gene circuit that can count up to 4. In essence, the counteruses two toggle switches, each storing 1 bit, to keep track of the 4 states. The design of the counter is highly modular, with the hope that it can be included as a unit in larger circuits, and also combined with further counter instances to keep track of a much larger number of states, up to (2^(n+1)) with n units. To facilitate further developments and integration to other projects, the counter is available in form of BioBricks. Among many exciting applications, the availability of a counter enables the execution of sequential instructions, and paves the way for the execution of artifical programs inside living cells.
Contents |
Introduction
The past few years have seen the emergence of the field of synthetic biology, in which functional units are designed and built into living cells to generate a particular behaviour, and ultimately to better understand Life's mechanisms. Previous efforts include the creation of gene circuits that generate oscillating behaviour (Elowitz00), toggle switch functionality (Atkinson03), artificial cell-cell communication (Bulter04) or pattern-forming behaviour (Basu2005). The present document describes the design and realization of a gene circuit that counts to 4.
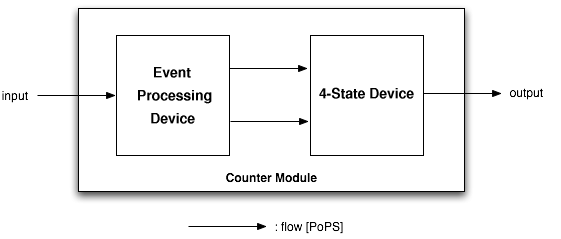
Design of the Counter
The counter is a genetic circuit that has 1 input and 4 outputs. It uses the input signal to switch from one of the four output to the next. When the input signal is high, either output 1 or 3 is active, when it is low, output 2 or 4 is active. Thus, output 1 and 3 alternatively keep track of high input signal, while output 2 and 4 alternatively keep track of low input signals.
As depicted above, the counter is made of two parts, serially linked:
- the "Input" module, which splits the input into two opposite signals.
- the "NOR" module, which uses these two signals to sequencially switch through the outputs 1, 2, 3 and 4.
Note that all interfaces have flows described in Polymerase Per Second (PoPS), is explained in details on the [http://partsregistry.org/cgi/htdocs/AbstractionHierarchy/index.cgi abstraction hierarchy] of the MIT Registry of Parts. For instance, the input can be of any nature as long as an adequate promoter is available (e.g. heat-shock using a sigma32 promoter, IPTG using a LacI promoter, AHL using quorum sensing promoters...)
Input Module
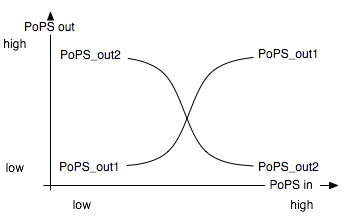
The input module splits the input into two opposite signals. It is best described through its system boundaries. One of the outputs should be high and the other low when S is high and vice versa when S is low:
Biological Implementation
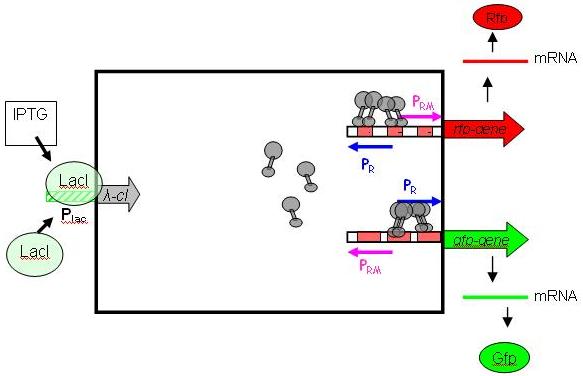
To achieve such behaviour, we use the λ-system, with IPTG as inductor. It is relatively easy to handle/debug, and does not restrict the module from being extended to work with other types of inputs. More importantly, it is already available as a BioBrick (Registry package 7.05) in its unidirectional flavour (In nature, the λ-system is bidirectional, with Pr on one DNA strand and Prm on the other, overlapping). The following picture shows the gene circuit of the input module in details:
cI is a dimer and regulates the activity of the two promoter regions, Pr and Prm, on the λ-system. Pr is constitutively active and is repressed when cI binds to the two operator regions it overlaps with (OR1, OR2). Conversly, Prm has low basal activity, and is activated by cI. Since the two promoters are regulated by the same protein-operator interactions, repression and activation is expected to be symmetrical (a necessary condition, see results from simulation below). For more details, please consult the page Input-module.
NOR Module
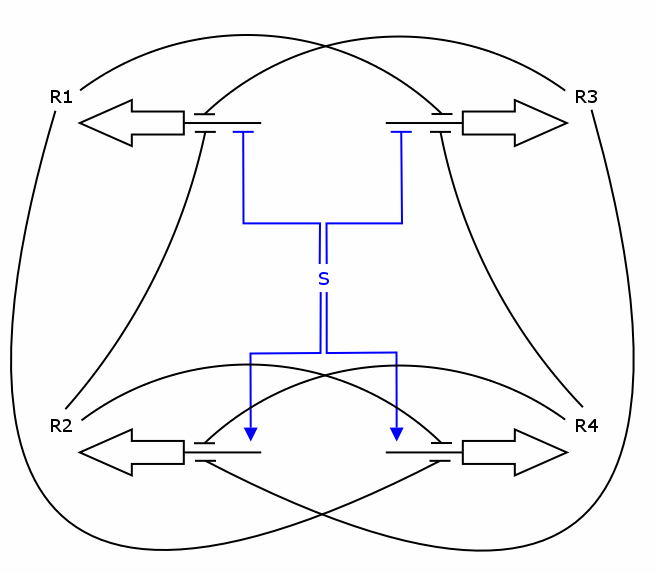
The "NOR" module uses two inputs to sequencially switch through its outputs 1, 2, 3 and 4. To achieve such behaviour, we use four interconnected "NOR" gates. In essence, a NOR gate is a component that has two inputs and one output, where the output is only high if none of the input is high. Concretly, a NOR gate can be implemented through a promoter with high basal activity that is repressed by two effectors. In the particular case, our NOR gates have three inputs (or effectors), none of which must be active for the gene to be expressed.
The following diagram (which should be redrawn using better tools than ASCII art) shows how the four NOR gates are interconnected:
R3 R2 R4 R1 R4 R3 R1 R2
| | | | | | | |
/|____ | | | | ____|\ /|____ | | | | ____|\
___/ R1 |_=_=___ ___=_=_| R3 \___ ___/ R2 |_=_=___ ___=_=_| R4 \___
\ ____| = = |____ / \ ____| = = |____ /
\| | | |/ \| | | |/
\ / \ /
\ / \ /
input 2 input 1
The design is highly symmetrical. We have 4 genes producing 4 repressor proteins R1, R2, R3 and R4. The production of each protein uses a constitutive promoter, which is down-regulated by 3 specific repressors, the two "following" repressors as well as either input 1 (for R2 and R4) or input 2 (for R1 and R3). By design of the input module, input 1 and input 2 have opposite activity, meaning that either R1/R3 or R2/R4 is active. Furthermore, since R1/R3 (respectively R2/R4) are repressing each other, only one of the two is active. Therefore, in a stable situation, only 1 of the 4 repressor proteins is expressed.
Let us assume that R1 is being expressed. Input 2 must then be low, and therefore input 1 high. This situation is stable and remains until there is a change in the inputs. Now, if input 1 decreases, and input 2 increases, the expression of R1 will come to a halt. Since input 1 is now low, either R2 or R4 will be expressed. At this stage, R1 is still present in relatively high concentration and by repressing R4, it tips the balance in favor of R2, leading to a new stable state in which only R2 is expressed.
Note that electrical engineers call such a device a "J-K flip flop". It can also be seen as a combination of two toggle switches (Atkinson03), each being able to store one bit.
Biological Implementation
We use zink-fingers proteins (ZFP) as repressors. This class of proteins bind to specific base pairs on the DNA. Many protein-DNA interaction for ZF domains and triplet of base pairs have been described, therefore making it possible to to construct artificial transcription factors by combining ZF domains in a modular fashion. The idea is to use a ZFP as a repressor by putting a binding site for a ZFP upstream of the coding region and thereby preventing RNA polymerase to transcribe the gene.
Simulation
The simulation was performed through a deterministic model using ordinary differential equations (ODEs), as this approach is commonly used in modelling gene networks. Recall the counter architecture:
(S is here the input of the counter. Note that the work of the input module is symbolized here by the dual effect of S, once as an activator and once as a repressor. In reality and as described in the section above, the input signal is converted to 2 opposite signals, both of them acting as repressors, alternatively.)
The 4 corresponding differential equations are:
dR1/dt = k_syn_R1 * rep(S) * rep(R2) * rep(R3) - k_deg_R1 * R1
dR2/dt = k_syn_R2 * act(S) * rep(R3) * rep(R4) - k_deg_R2 * R2
dR3/dt = k_syn_R3 * rep(S) * rep(R1) * rep(R4) - k_deg_R3 * R3
dR4/dt = k_syn_R4 * act(S) * rep(R1) * rep(R2) - k_deg_R4 * R4
\_________________ _________________/ \_______ _______/
V V
synthesis rate degradation rate
where act(A) = (K_act*A)^n / (1+(K_act*A)^n)
and rep(R) = 1 / (1+(K_rep*R)^n)
K are affinity constants, while k are kinetic constants.
Since R1 to R4 all use the same constitutive promoter, all kinetic constants k_syn_R* have the same value. Solving the system in Matlab using reasonable affinity and kinetic constants, the result can look as follows:
As expected, [R3] follows every second peak of [S].
By exploring the parameter space and performing Sensitivity Analysis, the following conclusions could be drawn:
- Changes in the affinity of the zink fingers affect the system more strongly than changes in the affinity of the input S.
- The affinity constants R1..R4 should be as symmetrical as possible, in particular the couples R1,R3 and R2,R4. A difference in the affinity constant up to an order of magnitude appears tolerable.
- ...
More details of the simulation work are reported on the page Modeling_and_overall_design.
Implementation
Results and Discussion
Applications and Perspectives
Abstract for Colloquium Calzone
The past few years have seen the emergence of the field of synthetic biology, in which functional units are designed and built into living cells to generate a particular behaviour, and ultimately to better understand Life's mechanisms. Previous efforts include the creation of gene circuits that generate oscillating behaviour, toggle switch functionality, artificial cell-cell communication or pattern-forming behaviour. This summer, a team of students from ETH worked on the design and implementation in-vivo of a gene circuit that counts up to 4, in the context of the international competition "iGEM", organized by MIT. Among many exciting applications, the availability of a counter enables the execution of sequential instructions, and paves the way for the execution of artifical programs inside living cells.