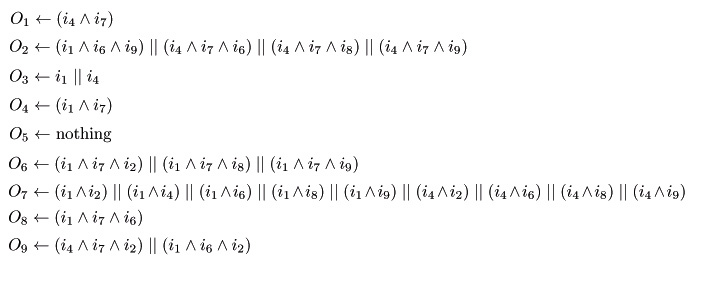Tokyo Alliance: Design/Method
From 2006.igem.org
| (55 intermediate revisions not shown) | |||
| Line 1: | Line 1: | ||
[[Image:tokyo_logomini.jpg|right]] | [[Image:tokyo_logomini.jpg|right]] | ||
| - | <center>[[Tokyo Alliance 2006|Top]] : [[Tokyo Alliance: Introduction|Introduction]] : [[Tokyo Alliance: Significance|Significance]] : [[Tokyo Alliance: Design/Method|Design/Method]] : [[Tokyo Alliance: Conclusion|Conclusion]] : [[About Tokyo Alliance]] </center> | + | <center>[[Tokyo Alliance 2006|Top]] : [[Tokyo Alliance: Introduction|Introduction]] : [[Tokyo Alliance: Significance|Significance]] : [[Tokyo Alliance: Design/Method|Design/Method]] : [[Tokyo Alliance: Conclusion|Results/Conclusion]] : [[About Tokyo Alliance]] </center> |
---- | ---- | ||
| - | |||
| - | |||
==Systematic design concept/method== | ==Systematic design concept/method== | ||
| - | === | + | ===Abstraction Phase=== |
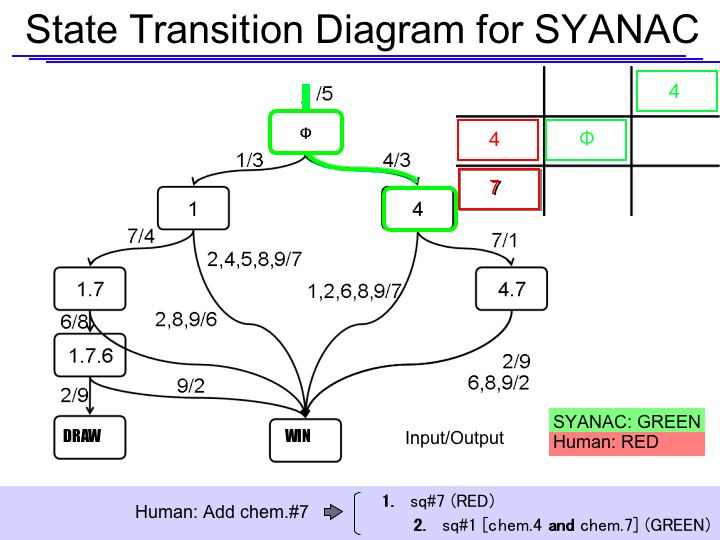
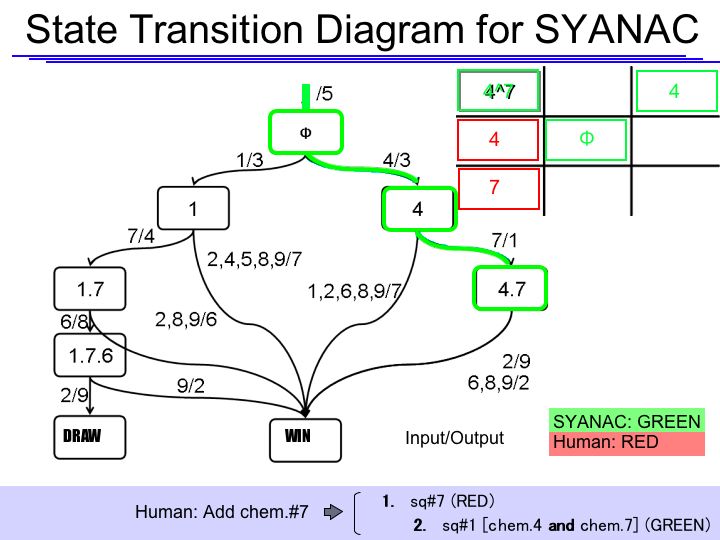
====State Transition Diagram==== | ====State Transition Diagram==== | ||
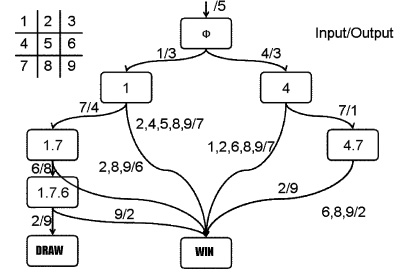
| - | [[Image:tokyo_statetransition.jpg|frame|State Transition Diagram]] | + | [[Image:tokyo_statetransition.jpg|frame|State Transition Diagram (SYANAC Side)]] |
*Combination of Noughts-and-Crosses | *Combination of Noughts-and-Crosses | ||
| Line 26: | Line 24: | ||
; 3rd: SYANAC must choose sq#3 | ; 3rd: SYANAC must choose sq#3 | ||
| - | *SYANAC | + | |
| - | **25 | + | Therefore, SYANAC's conbination patterns and inputs are as follows: |
| + | |||
| + | |||
| + | *SYANAC | ||
| + | **25 combination patterns(Eliminating symmetrical pairs) | ||
| + | **7 types of inputs | ||
| + | |||
The State Transition Diagram shown right describes SYANAC's behavior based on this rule. | The State Transition Diagram shown right describes SYANAC's behavior based on this rule. | ||
| + | |||
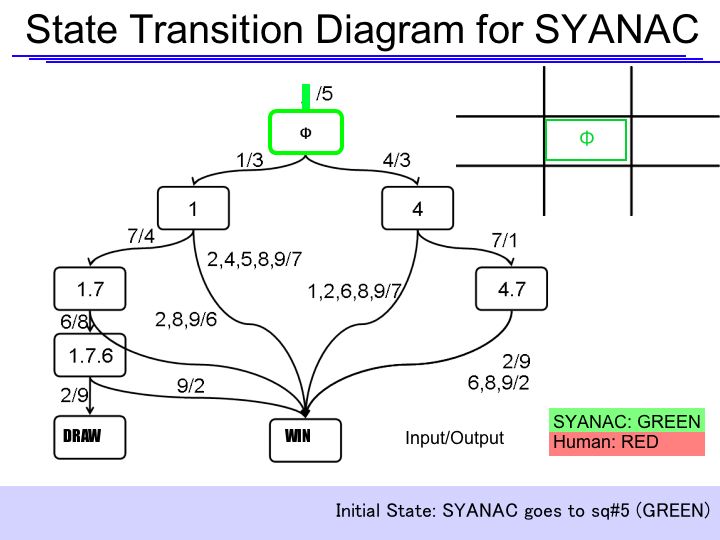
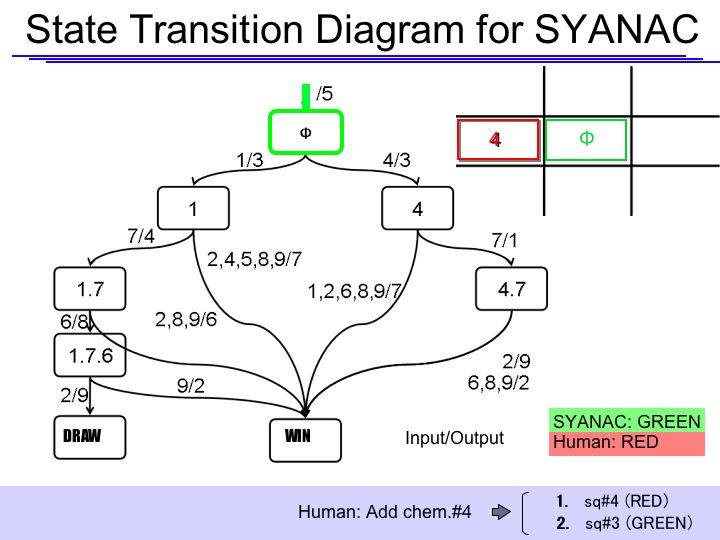
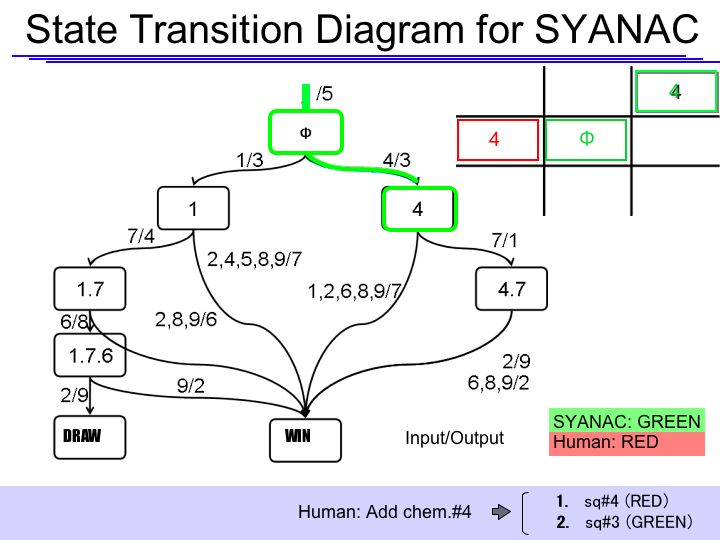
| + | =====State Transition Diagram Demonstration===== | ||
| + | |||
| + | [http://131.112.128.86/downloads/Tokyo_StateTransition.ppt State Transition Diagram Demo] (.ppt 528KB ver.1031) | ||
| + | |||
| + | <gallery> | ||
| + | Image:igem_tokyo_std_25.jpg | ||
| + | Image:igem_tokyo_std_26.jpg | ||
| + | Image:igem_tokyo_std_27.jpg | ||
| + | Image:igem_tokyo_std_28.jpg | ||
| + | Image:igem_tokyo_std_29.jpg | ||
| + | </gallery> | ||
| + | |||
| + | if we test all of the SYANAC's move, we can draw this STATE TRANSITION DIAGRAM for SYANAC. | ||
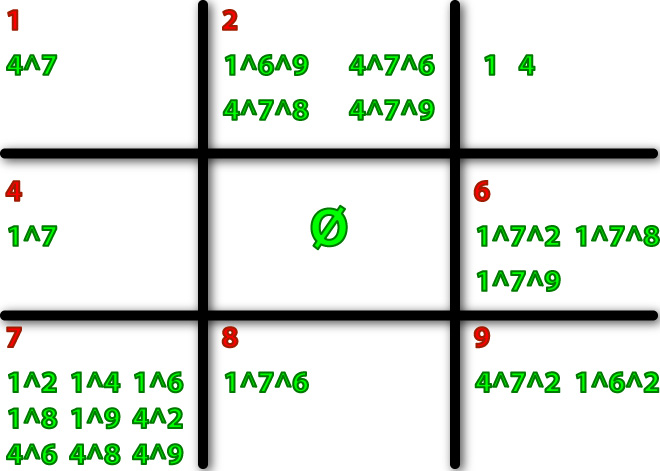
====Logic Gates==== | ====Logic Gates==== | ||
| - | |||
| + | When we examined ALL of the patterns in the State Transition Diagram, we can decide which logic gates we need in each square. | ||
| - | + | :[[Image:Tokyo_logiccatalog.jpg|300px|Logic Gates which have to be assigned to the squares]] | |
| - | ===Construction | + | Here we show you the logic gates of each sq# according to the state transition. |
| + | |||
| + | :[[Image:Tokyo_gates.jpg|Logic Gates]] | ||
| + | |||
| + | |||
| + | |||
| + | ====Block Diagram (System/Device)==== | ||
| + | |||
| + | *System | ||
| + | |||
| + | We determine each square as a system. (So we have to make 9 systems to make SYANAC.) We show some examples in figures below. | ||
| + | |||
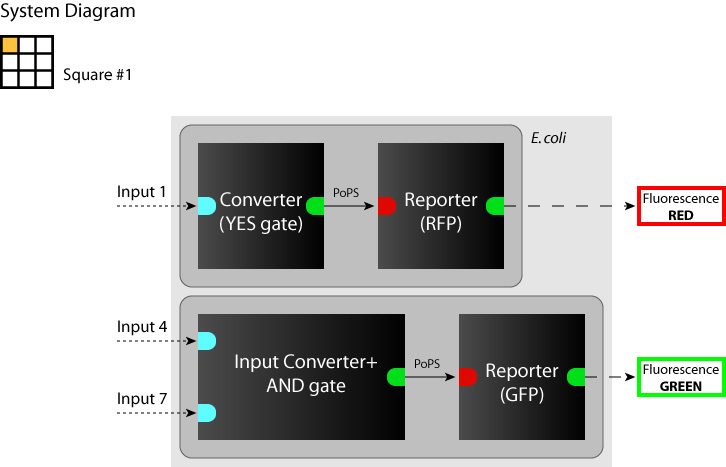
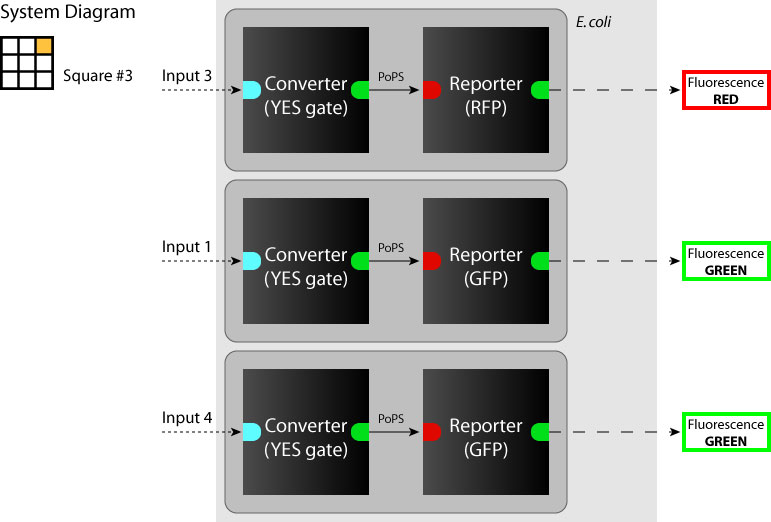
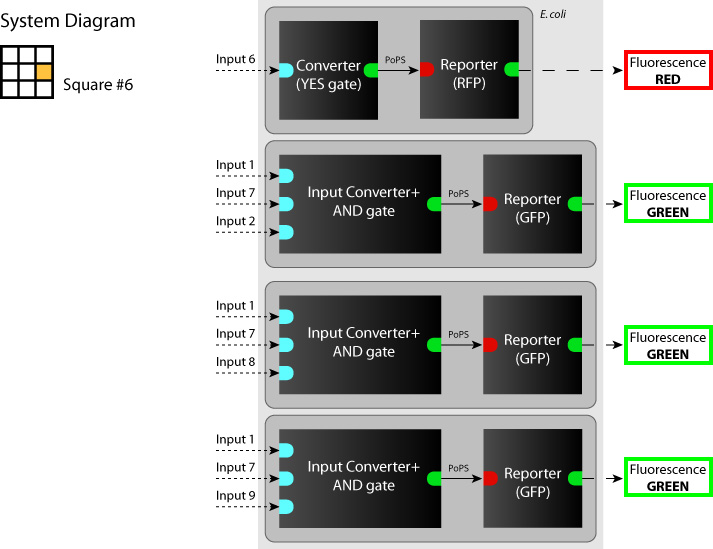
| + | :[[Image:Tokyo_dev_sq_1.jpg|250px|System diagram: sq#1]] [[Image:Tokyo_dev_sq_3.jpg|250px|System diagram: sq#3]] [[Image:Tokyo_dev_sq_6.jpg|250px|System diagram: sq#6]] | ||
| + | |||
| + | |||
| + | |||
| + | *Device | ||
| + | |||
| + | When we look at the Logic Gates inside all of the systems, they are all consisted of YES, AND, AND-AND Gates. | ||
| + | |||
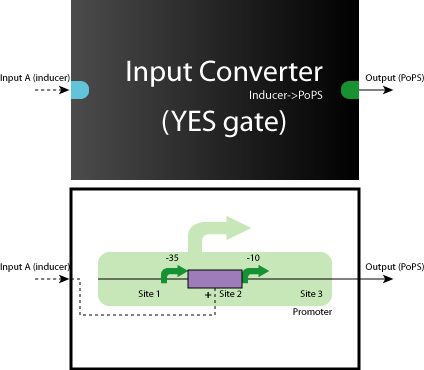
| + | :[[Image:Tokyo_dev_yes.jpg|250px|YES Gate]] [[Image:Tokyo_dev_and2.jpg|250px|AND Gate (2 inputs)]] | ||
| + | |||
| + | :[[Image:Tokyo_dev_and3_1.jpg|250px|AND Gate (3 inputs) <1>]] [[Image:Tokyo_dev_and3_2.jpg|250px|AND Gate (3 inputs) <2>]] | ||
| + | |||
| + | So, what we have to do is to construct these Logic Gates in a simple, systematic way. | ||
| + | |||
| + | ===Construction Phase=== | ||
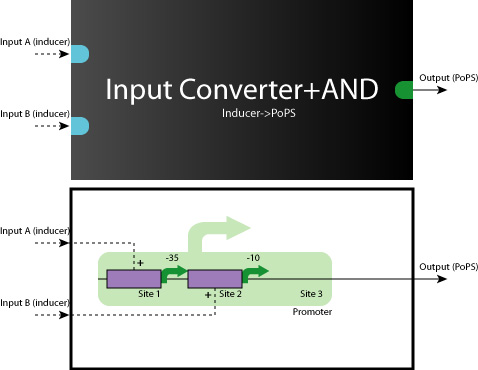
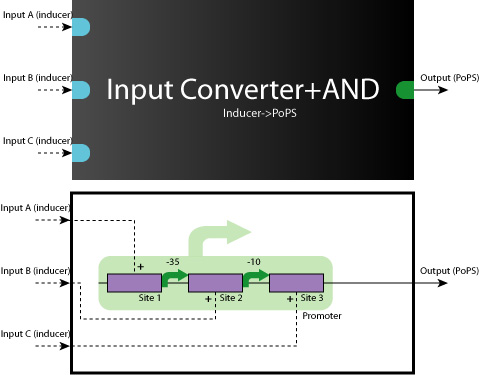
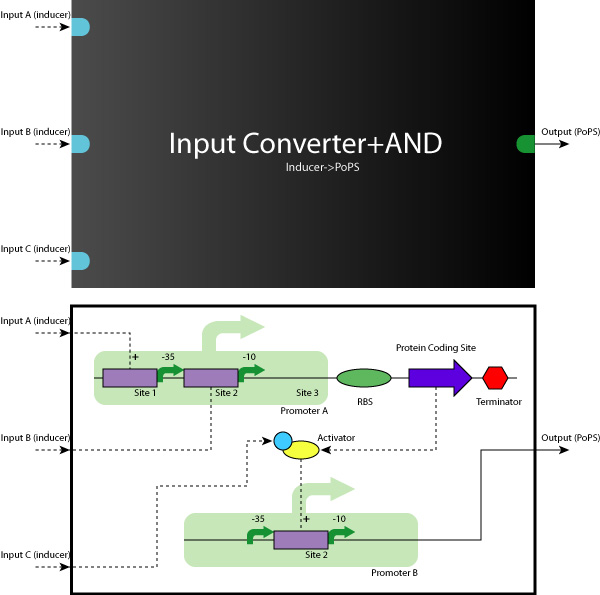
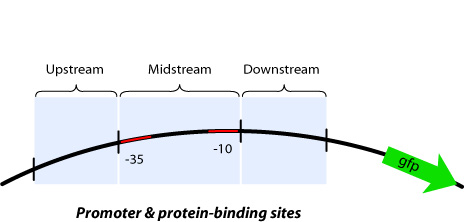
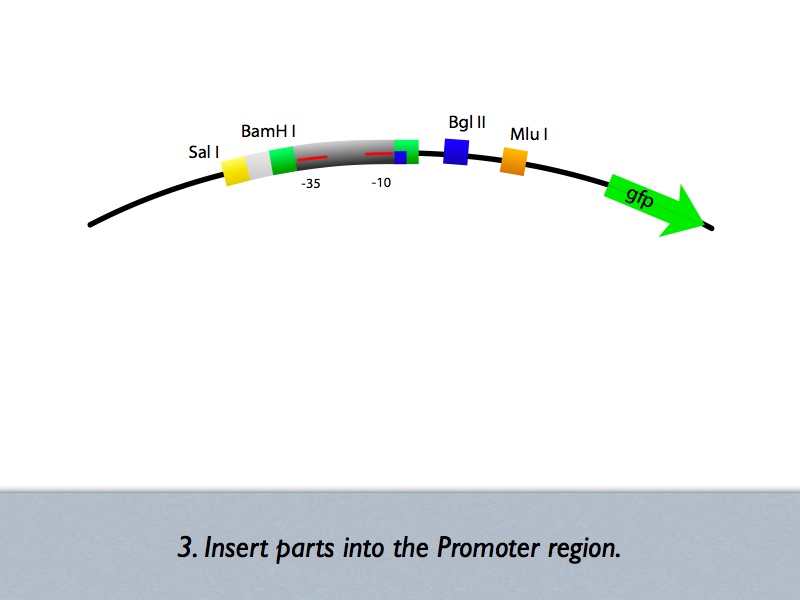
====Up/Mid/Downstream==== | ====Up/Mid/Downstream==== | ||
| + | :[[Image:Tokyo_construction_concept.jpg|Up/Mid/Downstream]] | ||
| + | |||
| + | |||
| + | In order to implement logic gates, combination of several kinds of regulator binding sites is necessary. For this reason, separated three regions named upstream, midstream, and downstream as shown in figure is added new prefixes and suffixes in each end. | ||
| + | |||
| + | |||
| + | |||
====working model==== | ====working model==== | ||
| + | |||
| + | Here we show you some typical working model examples of the Logic Gates. | ||
| + | |||
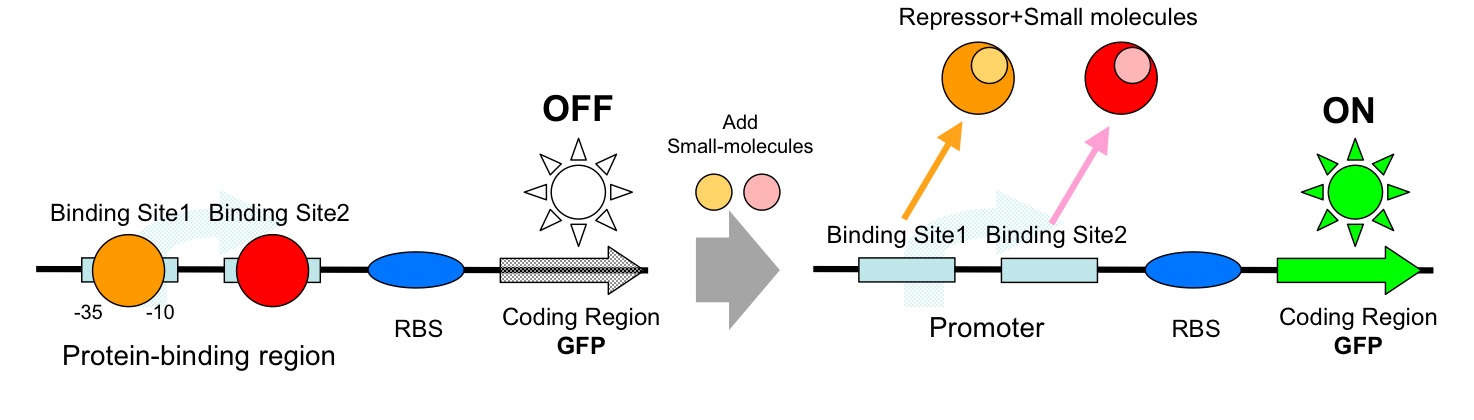
| + | *AND Gate (Repressor+Repressor) | ||
| + | |||
| + | :[[Image:tokyo_workingmodel_1.jpg|500px|AND-AND gate (Repressor+Repressor)]] | ||
| + | |||
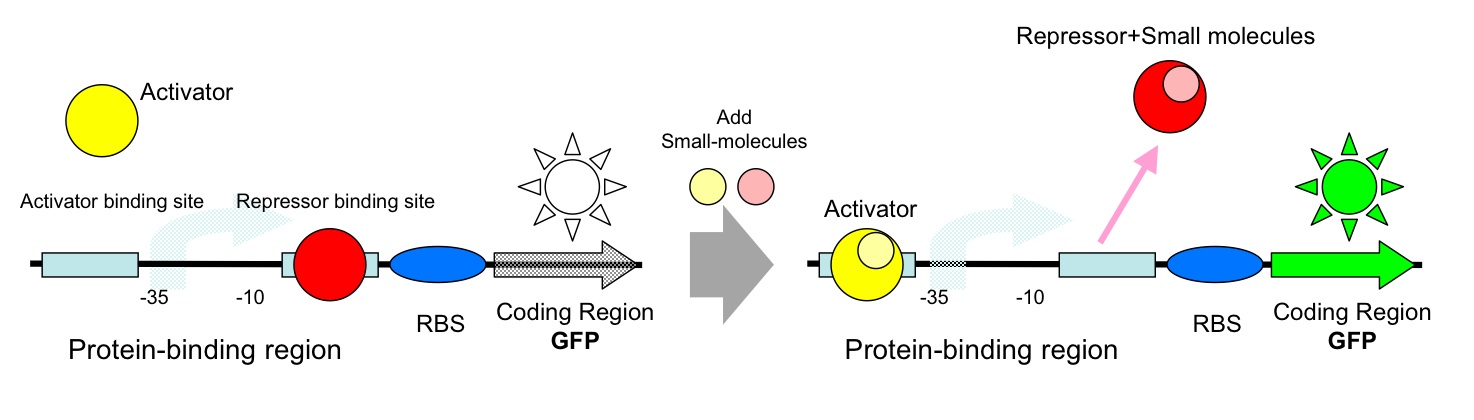
| + | *AND Gate (Activator+Repressor) | ||
| + | |||
| + | :[[Image:tokyo_workingmodel_2.jpg|500px|AND-AND gate (Activator+Repressor)]] | ||
| + | |||
| + | AND-AND Gates are also able to construct in the same way. | ||
| + | |||
====DNA Construction Procedure==== | ====DNA Construction Procedure==== | ||
| + | |||
| + | *Midstream Parts Insertion | ||
| + | |||
| + | :[http://131.112.128.86/downloads/tokyo_mid_insertion.mov Midstream Parts Insertion Procedure (.mov)] (Requires QuickTime) | ||
| + | |||
| + | <gallery> | ||
| + | Image: tokyo_procedure.001.jpg | ||
| + | Image: tokyo_procedure.002.jpg | ||
| + | Image: tokyo_procedure.003.jpg | ||
| + | Image: tokyo_procedure.004.jpg | ||
| + | </gallery> | ||
| + | |||
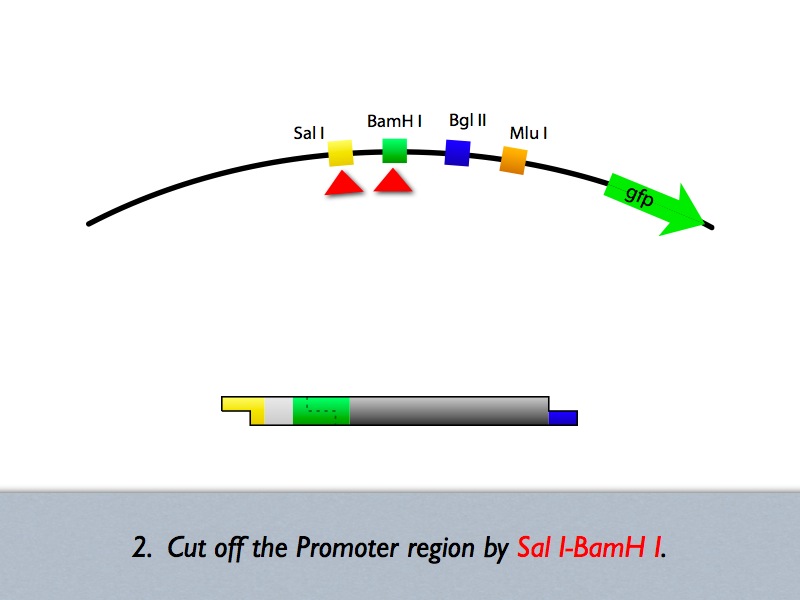
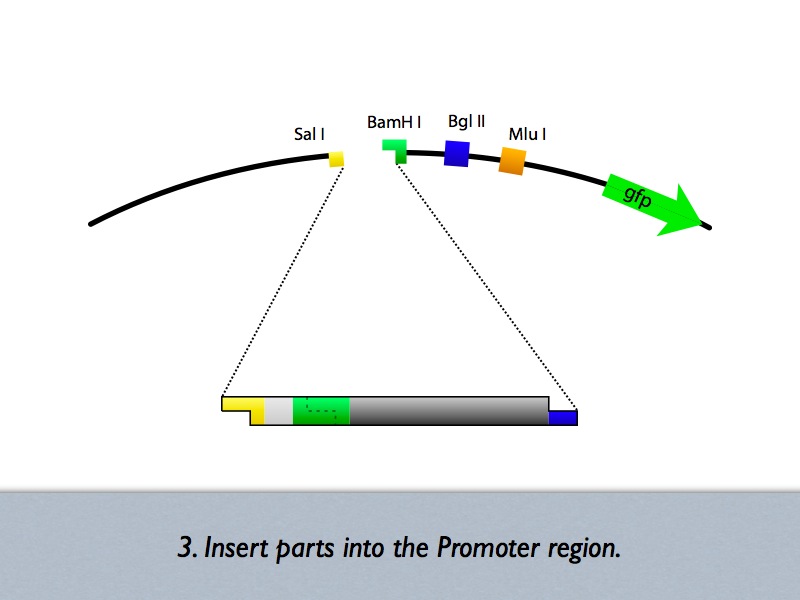
| + | Based on the iGEM construction method, divided three areas are generated new prefixes and suffixes. | ||
| + | The prefixes are SalI and BglII sites. The suffixes are BamHI and MluI sites. | ||
| + | Since, BamHI and BglII is compatible each other, we can insert several number of regulatory sequences purchased from oligo house into this area. | ||
| + | For midstream part, a protein binding sequence is inserted between SalI and BamHI sites. While the vector has SalI and BamHI as prefixes, insert has SalI and BglII sites on its ends. After ligation, BamHI site of the vector disappear and another sequence can be inserted in front of this sequence. | ||
| + | |||
| + | |||
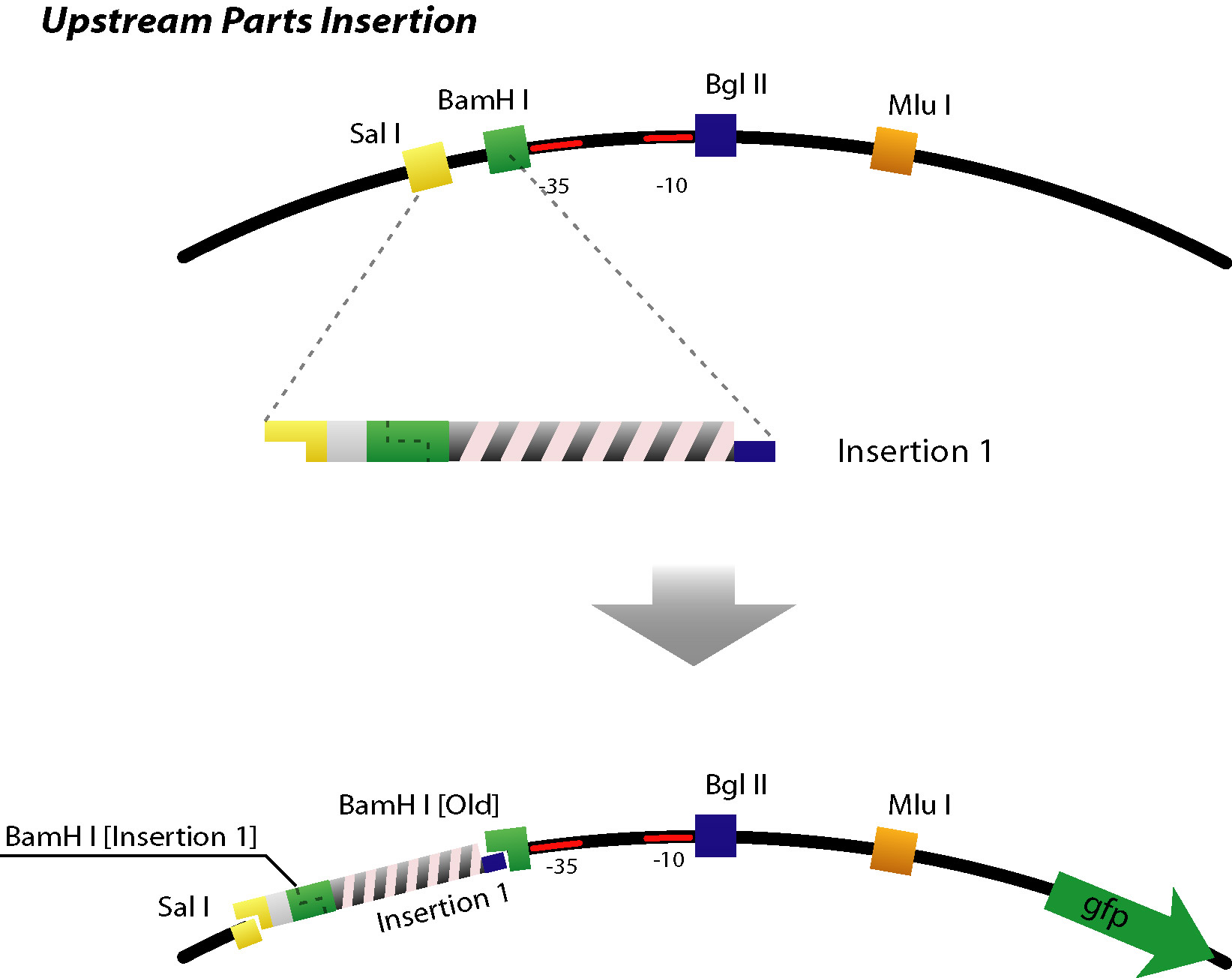
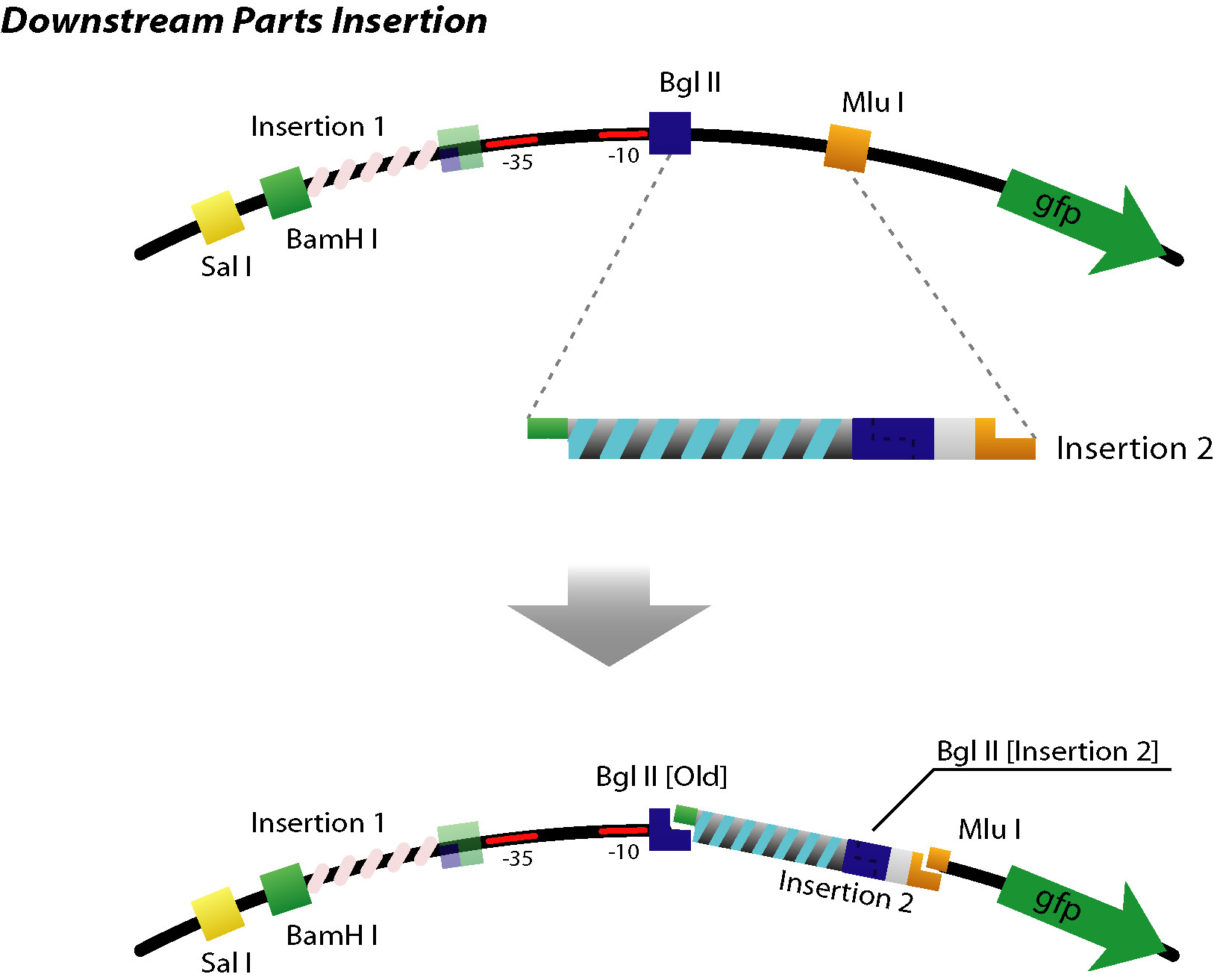
| + | *Up/Downstream Parts Insertion | ||
| + | |||
| + | |||
| + | :[[Image: tokyo_insert_up.jpg|500px|Upstream Parts Insertion]] | ||
| + | |||
| + | |||
| + | With this method, sequence for upstream area can be inserted in front of midstream area. | ||
| + | |||
| + | |||
| + | :[[Image: tokyo_insert_dn.jpg|500px|Downstream Parts Insertion]] | ||
| + | |||
| + | |||
| + | |||
| + | ::Next parts can be inserted with the same procedure. (Up/Downstream Insertion Parts) | ||
| + | |||
| + | |||
| + | On the other hand, in case of sequence for downstream, the sequence is inserted between BglII and MluI site in same method. | ||
| + | |||
| + | |||
| + | With our construction method, any number of regulatory sequences can be inserted into a promoter region* very easily. | ||
| + | |||
| + | (* We can systematically design promoter region which is recognised as 'one regulatory part' by the iGEM registry. | ||
| + | |||
| + | That means, our method enables us to construct promoter region in the lower level than the registry. | ||
| + | |||
| + | That is why that we are using different prefixes and suffixes to work seamlessly with the idea of iGEM parts.) | ||
Latest revision as of 15:22, 30 October 2006
Contents |
Systematic design concept/method
Abstraction Phase
State Transition Diagram
- Combination of Noughts-and-Crosses
- 362,880(=9!)[patterns] (sum up all patterns)
- 255,168 (As a game)
- 26,830 (Eliminating symmetrical pairs)
We added the following rules to reduce the number of transition functions and inputs.
- 1st
- SYANAC goes to the center of the board. (sq#5)
- 2nd
- Human goes to the specific corner(sq#1) or the edge(sq#4) of the board.
- 3rd
- SYANAC must choose sq#3
Therefore, SYANAC's conbination patterns and inputs are as follows:
- SYANAC
- 25 combination patterns(Eliminating symmetrical pairs)
- 7 types of inputs
The State Transition Diagram shown right describes SYANAC's behavior based on this rule.
State Transition Diagram Demonstration
[http://131.112.128.86/downloads/Tokyo_StateTransition.ppt State Transition Diagram Demo] (.ppt 528KB ver.1031)
if we test all of the SYANAC's move, we can draw this STATE TRANSITION DIAGRAM for SYANAC.
Logic Gates
When we examined ALL of the patterns in the State Transition Diagram, we can decide which logic gates we need in each square.
Here we show you the logic gates of each sq# according to the state transition.
Block Diagram (System/Device)
- System
We determine each square as a system. (So we have to make 9 systems to make SYANAC.) We show some examples in figures below.
- Device
When we look at the Logic Gates inside all of the systems, they are all consisted of YES, AND, AND-AND Gates.
So, what we have to do is to construct these Logic Gates in a simple, systematic way.
Construction Phase
Up/Mid/Downstream
In order to implement logic gates, combination of several kinds of regulator binding sites is necessary. For this reason, separated three regions named upstream, midstream, and downstream as shown in figure is added new prefixes and suffixes in each end.
working model
Here we show you some typical working model examples of the Logic Gates.
- AND Gate (Repressor+Repressor)
- AND Gate (Activator+Repressor)
AND-AND Gates are also able to construct in the same way.
DNA Construction Procedure
- Midstream Parts Insertion
- [http://131.112.128.86/downloads/tokyo_mid_insertion.mov Midstream Parts Insertion Procedure (.mov)] (Requires QuickTime)
Based on the iGEM construction method, divided three areas are generated new prefixes and suffixes. The prefixes are SalI and BglII sites. The suffixes are BamHI and MluI sites. Since, BamHI and BglII is compatible each other, we can insert several number of regulatory sequences purchased from oligo house into this area. For midstream part, a protein binding sequence is inserted between SalI and BamHI sites. While the vector has SalI and BamHI as prefixes, insert has SalI and BglII sites on its ends. After ligation, BamHI site of the vector disappear and another sequence can be inserted in front of this sequence.
- Up/Downstream Parts Insertion
With this method, sequence for upstream area can be inserted in front of midstream area.
- Next parts can be inserted with the same procedure. (Up/Downstream Insertion Parts)
On the other hand, in case of sequence for downstream, the sequence is inserted between BglII and MluI site in same method.
With our construction method, any number of regulatory sequences can be inserted into a promoter region* very easily.
(* We can systematically design promoter region which is recognised as 'one regulatory part' by the iGEM registry.
That means, our method enables us to construct promoter region in the lower level than the registry.
That is why that we are using different prefixes and suffixes to work seamlessly with the idea of iGEM parts.)