Brown:Tri-Stable toggle switch
From 2006.igem.org
(→Future work) |
|||
| (9 intermediate revisions not shown) | |||
| Line 5: | Line 5: | ||
[[Image:Tristable_Toggle.jpg|left|500px|A general tri-stable toggle]] | [[Image:Tristable_Toggle.jpg|left|500px|A general tri-stable toggle]] | ||
| + | |||
Our implementation uses the pLac, pTet, and pBad/AraC promoters and their respective inhibiting proteins. We chose these because of the relative ease with which each promoter is induced: by adding IPTG for the pLac-promoted region, tetracycline for the PTet-promoted region, and arabinose for the pBad/Ara genes. By characterizing each of the three pathways without following genes and terminators, we enable a tri-stable switching network of any three biobricks to be constructed with minimal cloning. | Our implementation uses the pLac, pTet, and pBad/AraC promoters and their respective inhibiting proteins. We chose these because of the relative ease with which each promoter is induced: by adding IPTG for the pLac-promoted region, tetracycline for the PTet-promoted region, and arabinose for the pBad/Ara genes. By characterizing each of the three pathways without following genes and terminators, we enable a tri-stable switching network of any three biobricks to be constructed with minimal cloning. | ||
| Line 10: | Line 11: | ||
[[Image:Registry_tristable.jpg|Our implementation]] | [[Image:Registry_tristable.jpg|Our implementation]] | ||
| - | |||
| - | |||
<br><br> | <br><br> | ||
| - | + | Link to tri-stable switch on the registry:[http://partsregistry.org/Part:BBa_J24672 Tri-stable Switch] | |
| - | + | ||
| + | |||
| + | |||
| + | |||
=Modeling the tri-stable toggle switch= | =Modeling the tri-stable toggle switch= | ||
While the tri-stable switch is seemingly simple in design, just like any other system it is subject to potentially comprising factors such as promoter leakiness and other stochastic fluctuations. In an attempt to predict the behavior of the tri-stable switch, we created a deterministic model of the system taking into account these factors. The model structure is based on that described in "Prediction and measurement of an autoregulatory genetic module" by Farren Isaacs, et al. This paper features an excellent supplement that takes you hand-in-hand through the derivation of model equations. I will attempt to emulate this derivation with our model below. It is important to note that while we have some preliminary results, our model is very much a work in progress. In order to model the system accurately, many of the fundamental constants governing the model will need to be determined experimentally. For now we have used some constants from the literature and estimated some based on similar the values of similar constants also from the literature. | While the tri-stable switch is seemingly simple in design, just like any other system it is subject to potentially comprising factors such as promoter leakiness and other stochastic fluctuations. In an attempt to predict the behavior of the tri-stable switch, we created a deterministic model of the system taking into account these factors. The model structure is based on that described in "Prediction and measurement of an autoregulatory genetic module" by Farren Isaacs, et al. This paper features an excellent supplement that takes you hand-in-hand through the derivation of model equations. I will attempt to emulate this derivation with our model below. It is important to note that while we have some preliminary results, our model is very much a work in progress. In order to model the system accurately, many of the fundamental constants governing the model will need to be determined experimentally. For now we have used some constants from the literature and estimated some based on similar the values of similar constants also from the literature. | ||
| - | ==Derivation of the Model Equations== | + | ====Derivation of the Model Equations==== |
[[Derivation of the Model Equations]] | [[Derivation of the Model Equations]] | ||
| - | ==Table of preliminary model constants== | + | ====Table of preliminary model constants==== |
[[Table of preliminary model constants]] | [[Table of preliminary model constants]] | ||
Latest revision as of 05:31, 12 November 2006
Contents |
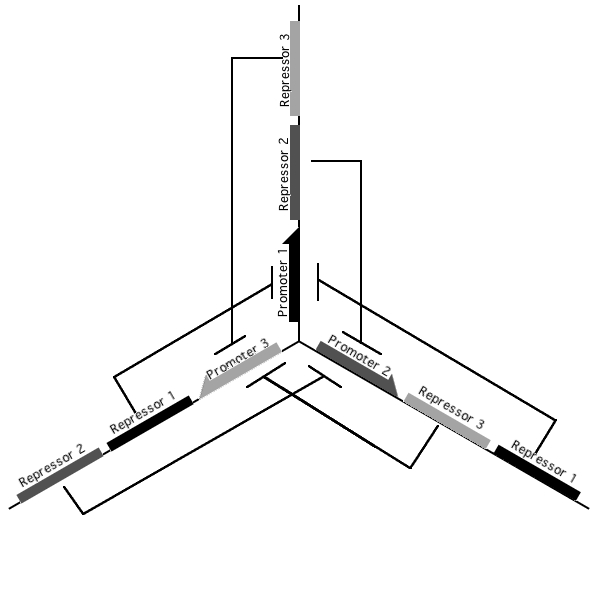
A tri-stable toggle switch
Pursuant to the the 1999 paper "Construction of a genetic toggle switch in Escherichia coli," by Timothy S. Gardner, Charles R. Cantor and James J. Collins, we wondered if the bi-stable toggle switch could be generalized to an n-stable switch. To that end, we conceived and began construction of the tri-stable toggle switch. The general idea is that when a selected promoter is activated, it represses the other two. As such each of the three states of our network are self-stabilizing.
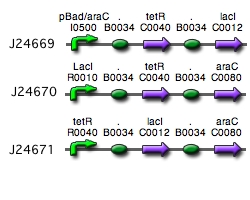
Our implementation uses the pLac, pTet, and pBad/AraC promoters and their respective inhibiting proteins. We chose these because of the relative ease with which each promoter is induced: by adding IPTG for the pLac-promoted region, tetracycline for the PTet-promoted region, and arabinose for the pBad/Ara genes. By characterizing each of the three pathways without following genes and terminators, we enable a tri-stable switching network of any three biobricks to be constructed with minimal cloning.
Link to tri-stable switch on the registry:[http://partsregistry.org/Part:BBa_J24672 Tri-stable Switch]
Modeling the tri-stable toggle switch
While the tri-stable switch is seemingly simple in design, just like any other system it is subject to potentially comprising factors such as promoter leakiness and other stochastic fluctuations. In an attempt to predict the behavior of the tri-stable switch, we created a deterministic model of the system taking into account these factors. The model structure is based on that described in "Prediction and measurement of an autoregulatory genetic module" by Farren Isaacs, et al. This paper features an excellent supplement that takes you hand-in-hand through the derivation of model equations. I will attempt to emulate this derivation with our model below. It is important to note that while we have some preliminary results, our model is very much a work in progress. In order to model the system accurately, many of the fundamental constants governing the model will need to be determined experimentally. For now we have used some constants from the literature and estimated some based on similar the values of similar constants also from the literature.
Derivation of the Model Equations
Derivation of the Model Equations
Table of preliminary model constants
Table of preliminary model constants
Preliminary modeling results
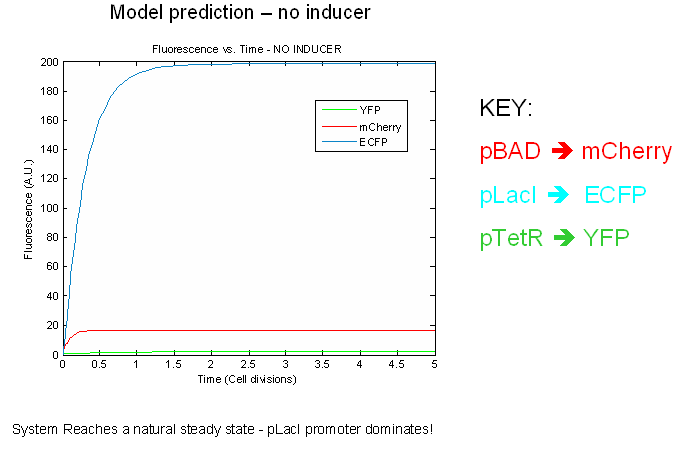
The preliminary modeling results predict things about of the the tri-stable switch. First of all, the model confirms certain obvious points such as the a shift to the proper steady expression state in the presence of inducers. This prediction attests to model validity more than anything else. Secondly, the model predicts that the switch will reach a natural steady state with one promoter dominating in the absence of inducers. This makes intuitive sense as the individual promoters will most likely have different strengths.
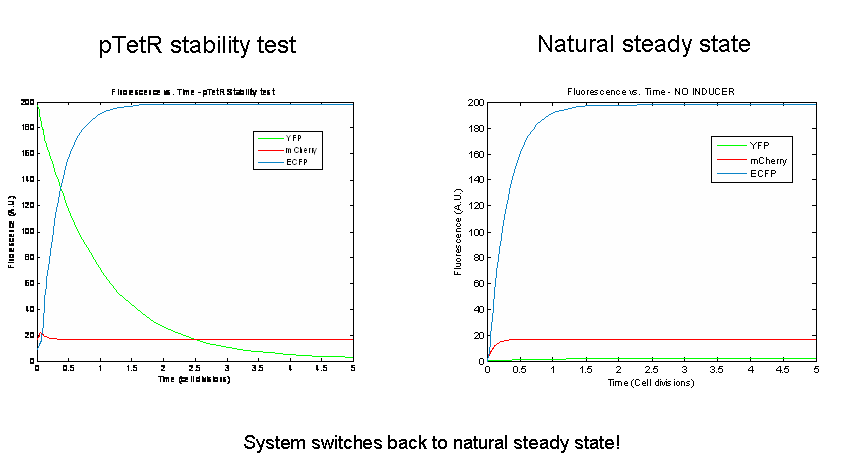
Next we tested the stability of the model by plugging in final steady-state induced levels of protein into an inducer-less system. The model predicts that the system will not remain stable and will instead revert back to the natural steady state for the inducer-less system. Even after changing several model parameters, the switch would not remain stable.
As a test of the model, models of the three potential bi-stable switches (already proven to be successful experimentally) using the same components and parameters were tested. In accordance with the literature, each of these constructs maintained stable expression of the induced state following the removal of the inducer. In order to probe the instability of the tri-stable switch further, tri-stable switches in which all of the components were effectively the same were created (ex:for all LacI-like, TetR and AraC were modeled as forming tetramers and having one operator.) Each of these systems reached a steady state in which all of the proteins evolved identically and were present at the same levels in the absence of inducer. The same stability tests were then performed. All of the constructs remained stable. Thus our model suggests that the similarity of the repressor-expression systems dominates the success or failure of the tri-stable switch. Furthermore, the bi-stable switch is less sensitive to this factor.
It should be noted that this is only a preliminary model. The values obtained from the literature will most like differ in our system. Through future experimentation we will elucidate these values and thus create a more accurate model. We will also conduct parameter scans aimed to provide further insight into the necessary system requirements for "tri-stability."
Link to MATLAB code for tri-stable model Media:tristable1.txt
Note: copy this code into MATLAB and save as an M-file
What we achieved
A successfully ligated pBad/arac construct in addition to partially completed ligations for the pLacI and the pTetR constructs were the results of our summer and semesters' work. The tri-stable toggle switch system was also modeled and proved to yield significant findings.
Challenges
Despite many cloning and ligation attempts, we were unable to create each component of the switch. More specifically, the pLacI and the pTetR circuits presented many ligation difficulties and proved to yield unsuccessful cloning. However, the pBAD/araC circuit was successfully constructed (yay!).
Conclusions
With the bigger picture in mind,this project yielded many successful outcomes.Firstly, we were able to successfully construct one of the three constructs necessary for a fully functional tri-stable toggle switch. Secondly, we were able to add more working parts to the registry, both a fully functioning pBad/AraC construct and many parts that were successfully ligated in the process of assembling the other two constructs. These parts will be used in the future by our team and perhaps many others as new ideas and projects develop. Also, it is necessary to mention our most recent finding from the modeling results for the tri-stable toggle switch. Interestingly enough, our model suggests that it is biologically unfeasible to create a switch with more than two components. If more than two components are introduced, such as three, the system is unable to maintain any one state and it will revert back to expressing its most dominant promoter construct. We find such results quite meaningful in demonstrating the biological limits of a system under study.
Future work
In the coming months, it is hoped that the failure of the ligation strategies for the pLacI and the pTetR constructs can be further investigated. We feel confident that we can continue to build from the one successful construction,the pBad/Arac construct and complete the other 2 constructs. To this end, it will be necessary to further troubleshoot the possible reasons why the cloning of the ligations were unsuccessful. Also we plan to conduct various experiments to elucidate more accurate model parameters specific to our system. Furthermore we will perform a parameter scan to investigate the determinates of "tri-stability."