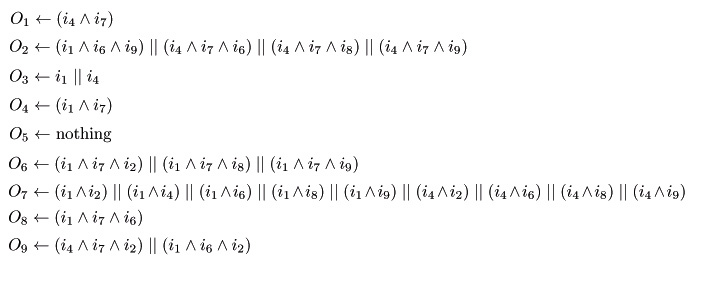Tokyo Alliance: Design/Method
From 2006.igem.org
| Line 61: | Line 61: | ||
*System | *System | ||
| + | |||
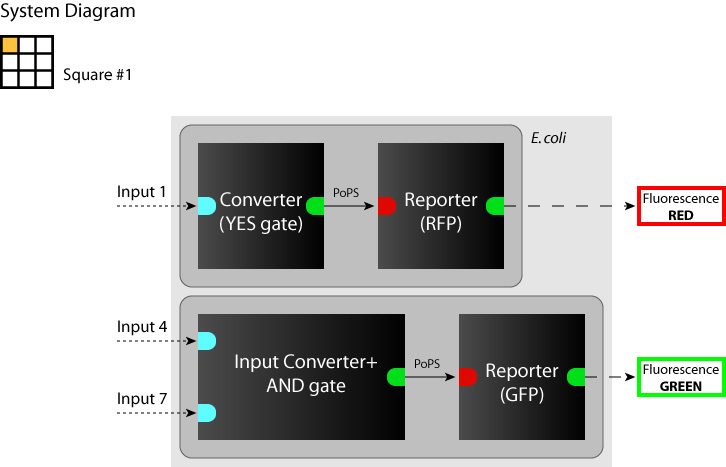
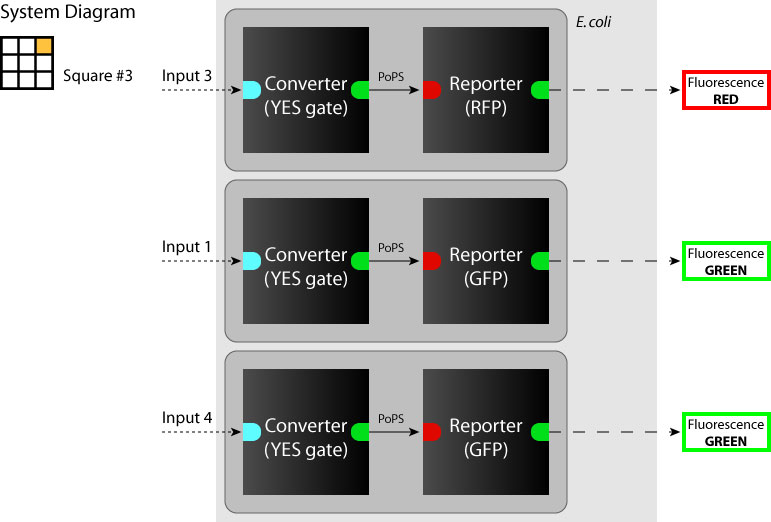
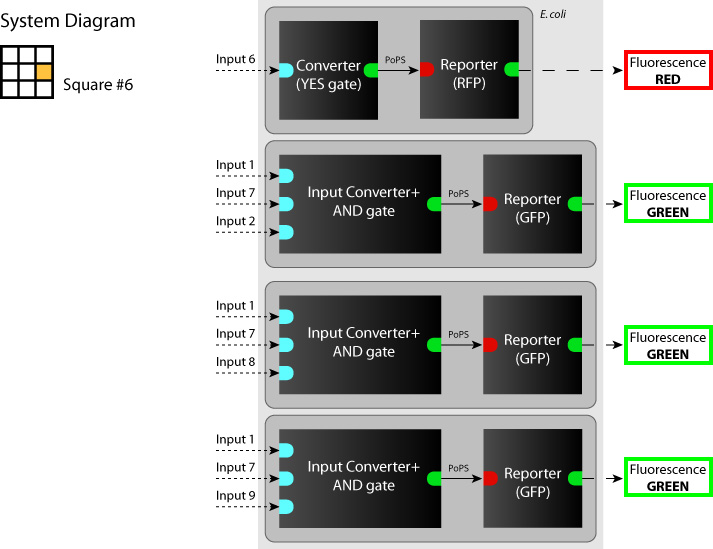
| + | We determine each square as a system. (So we have to make 9 systems to make SYANAC.) We show some examples on the figure below. | ||
| + | |||
:[[Image:Tokyo_dev_sq_1.jpg|250px|System diagram: sq#1]] [[Image:Tokyo_dev_sq_3.jpg|250px|System diagram: sq#3]] [[Image:Tokyo_dev_sq_6.jpg|250px|System diagram: sq#6]] | :[[Image:Tokyo_dev_sq_1.jpg|250px|System diagram: sq#1]] [[Image:Tokyo_dev_sq_3.jpg|250px|System diagram: sq#3]] [[Image:Tokyo_dev_sq_6.jpg|250px|System diagram: sq#6]] | ||
| Line 66: | Line 69: | ||
*Device | *Device | ||
| + | |||
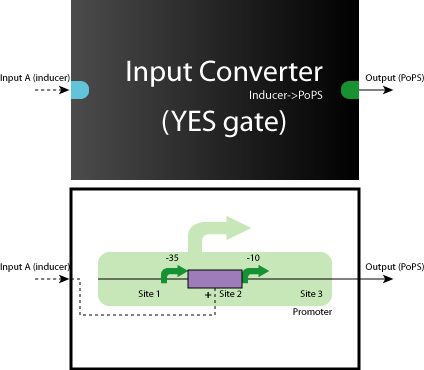
| + | When we look at the Logic Gates of all 9 systems, they are all consisted of YES, AND, AND-AND Gates. | ||
| + | |||
:[[Image:Tokyo_dev_yes.jpg|250px|YES Gate]] [[Image:Tokyo_dev_and2.jpg|250px|AND Gate (2 inputs)]] | :[[Image:Tokyo_dev_yes.jpg|250px|YES Gate]] [[Image:Tokyo_dev_and2.jpg|250px|AND Gate (2 inputs)]] | ||
:[[Image:Tokyo_dev_and3_1.jpg|250px|AND Gate (3 inputs) <1>]] [[Image:Tokyo_dev_and3_2.jpg|250px|AND Gate (3 inputs) <2>]] | :[[Image:Tokyo_dev_and3_1.jpg|250px|AND Gate (3 inputs) <1>]] [[Image:Tokyo_dev_and3_2.jpg|250px|AND Gate (3 inputs) <2>]] | ||
| - | + | So, what we have to do is to construct these Logic Gates in a simple, systematic way. | |
===Construction Phase=== | ===Construction Phase=== | ||
Revision as of 20:19, 29 October 2006
Contents |
Systematic design concept/method
Abstraction Phase
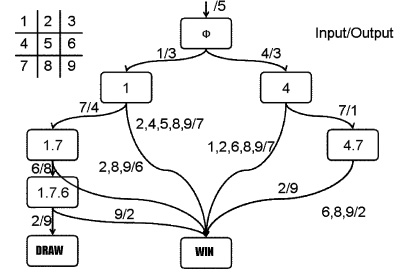
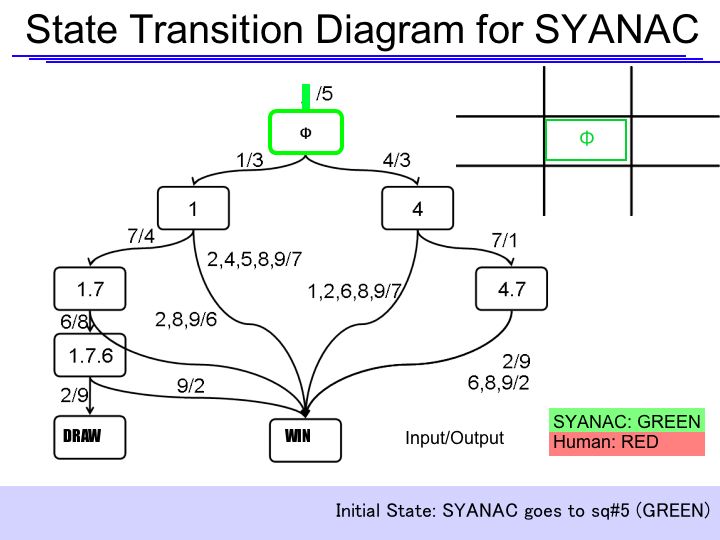
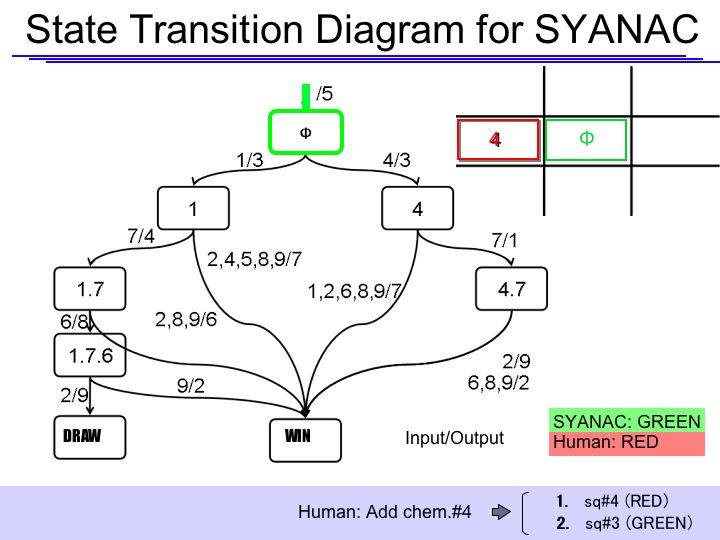
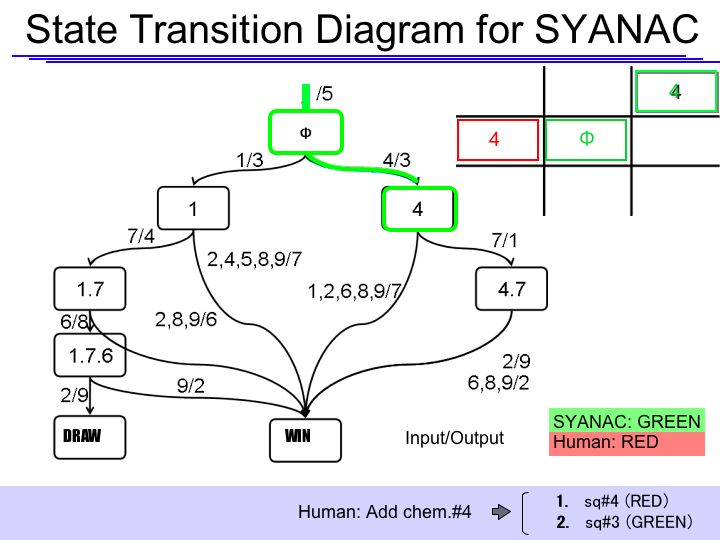
State Transition Diagram
- Combination of Noughts-and-Crosses
- 362,880(=9!)[patterns] (sum up all patterns)
- 255,168 (As a game)
- 26,830 (Eliminating symmetrical pairs)
We added the following rules to reduce the number of transition functions and inputs.
- 1st
- SYANAC goes to the center of the board. (sq#5)
- 2nd
- Human goes to the specific corner(sq#1) or the edge(sq#4) of the board.
- 3rd
- SYANAC must choose sq#3
Therefore, SYANAC's conbination patterns and inputs are as follows:
- SYANAC
- 25 combination patterns(Eliminating symmetrical pairs)
- 7 types of inputs
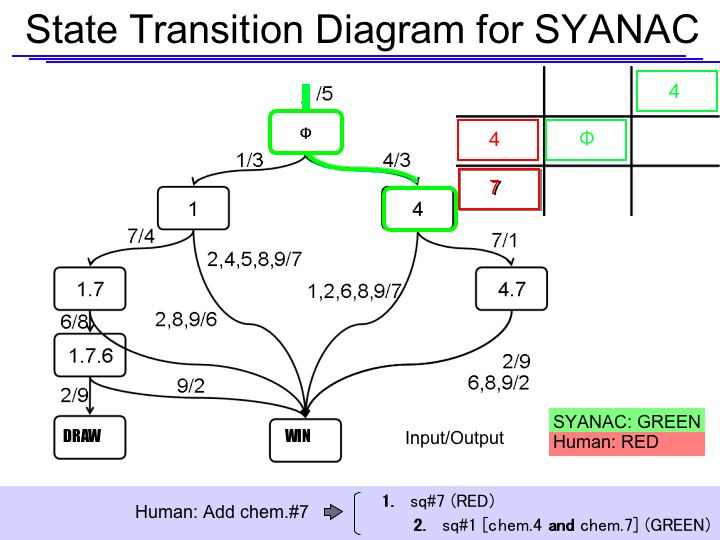
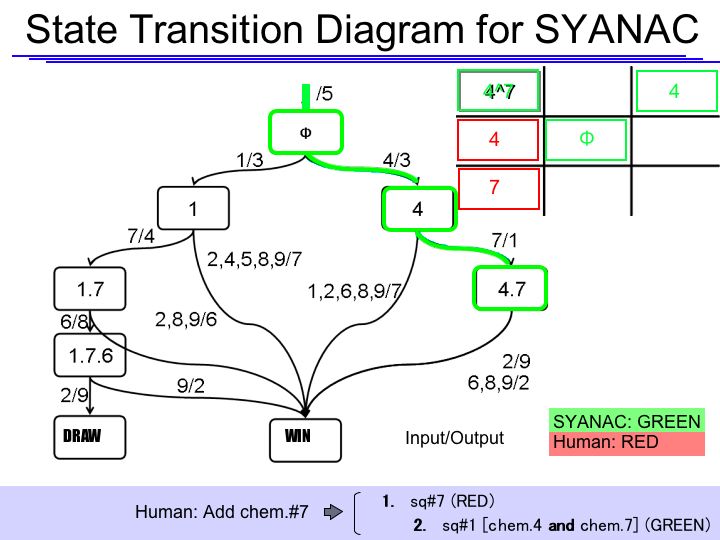
The State Transition Diagram shown right describes SYANAC's behavior based on this rule.
State Transition Diagram Demonstration
if we test all of the SYANAC's move, we can draw this STATE TRANSITION DIAGRAM for SYANAC.
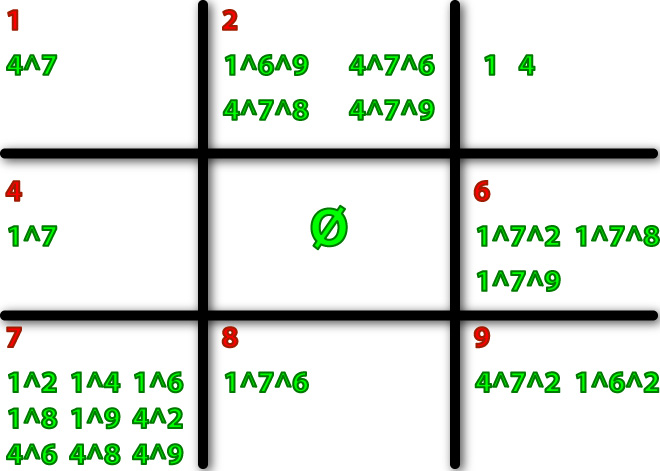
Logic Gates
When we examined ALL of the patterns in the State Transition Diagram, logic gates we need inside in each square will be like this.
Here we show you the logic gates of each sq# according to the state transition.
Block Diagram (System/Device)
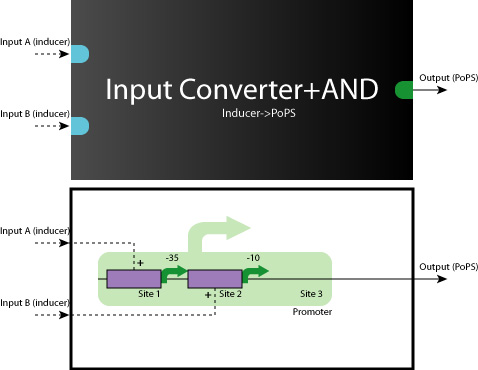
- System
We determine each square as a system. (So we have to make 9 systems to make SYANAC.) We show some examples on the figure below.
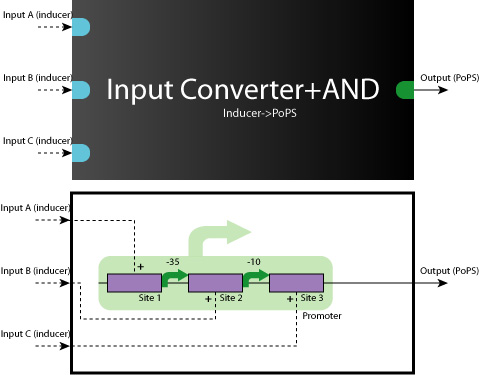
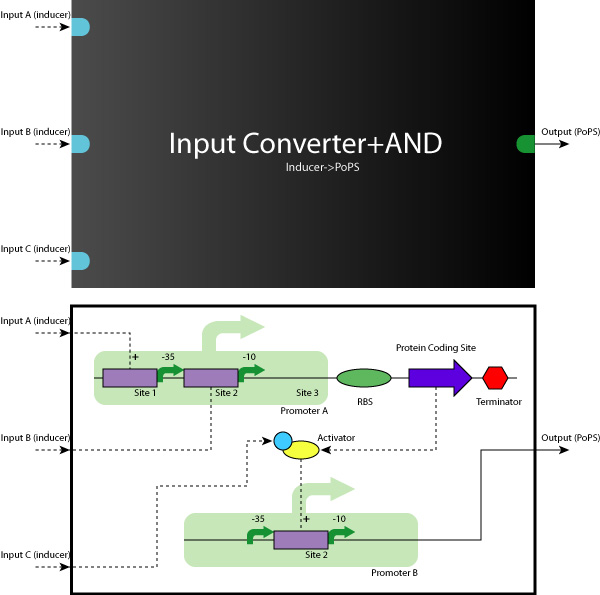
- Device
When we look at the Logic Gates of all 9 systems, they are all consisted of YES, AND, AND-AND Gates.
So, what we have to do is to construct these Logic Gates in a simple, systematic way.
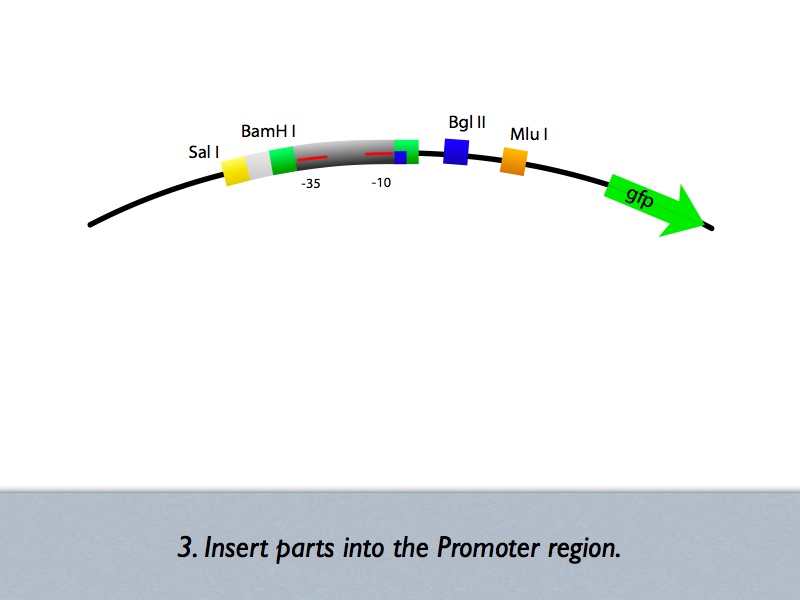
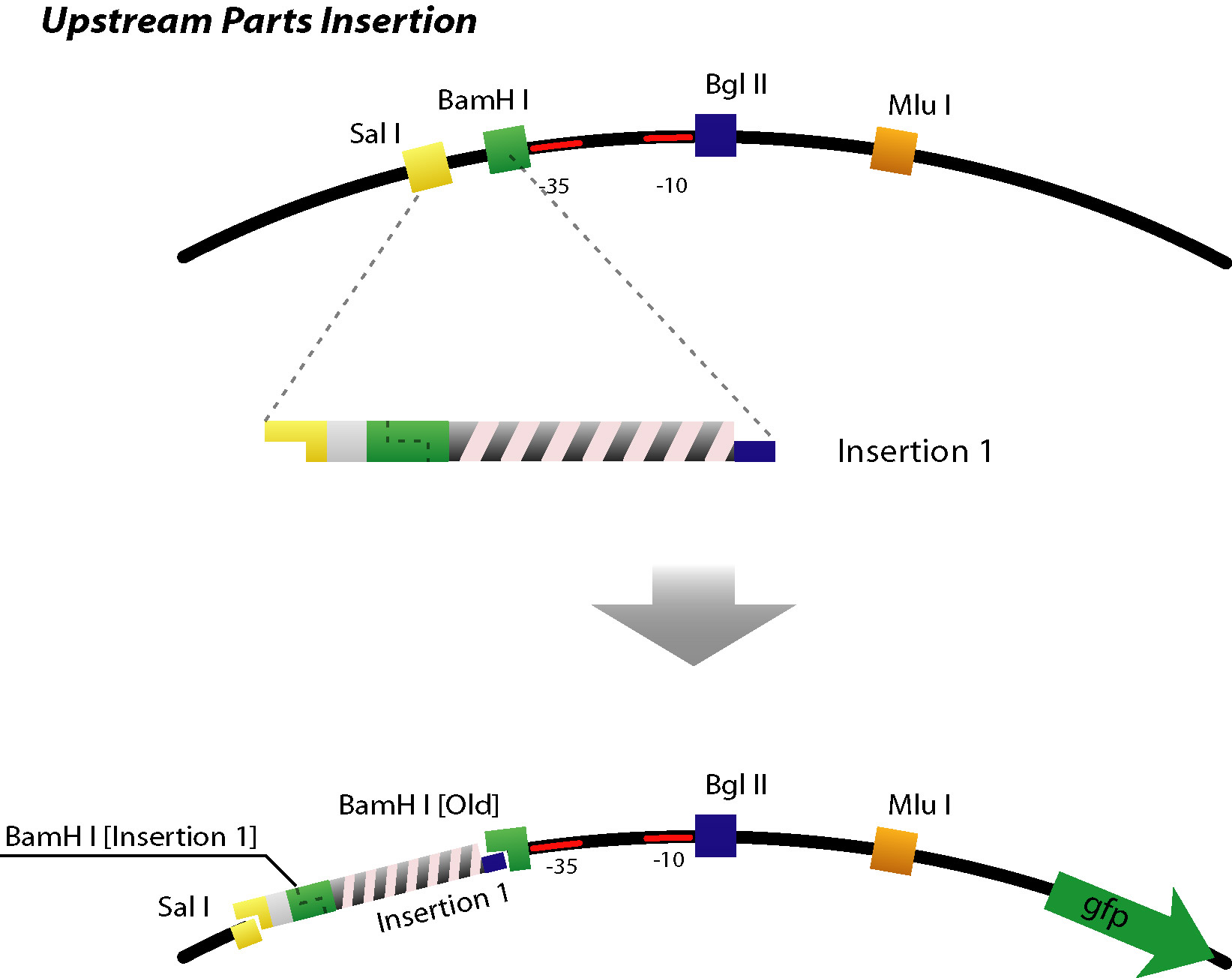
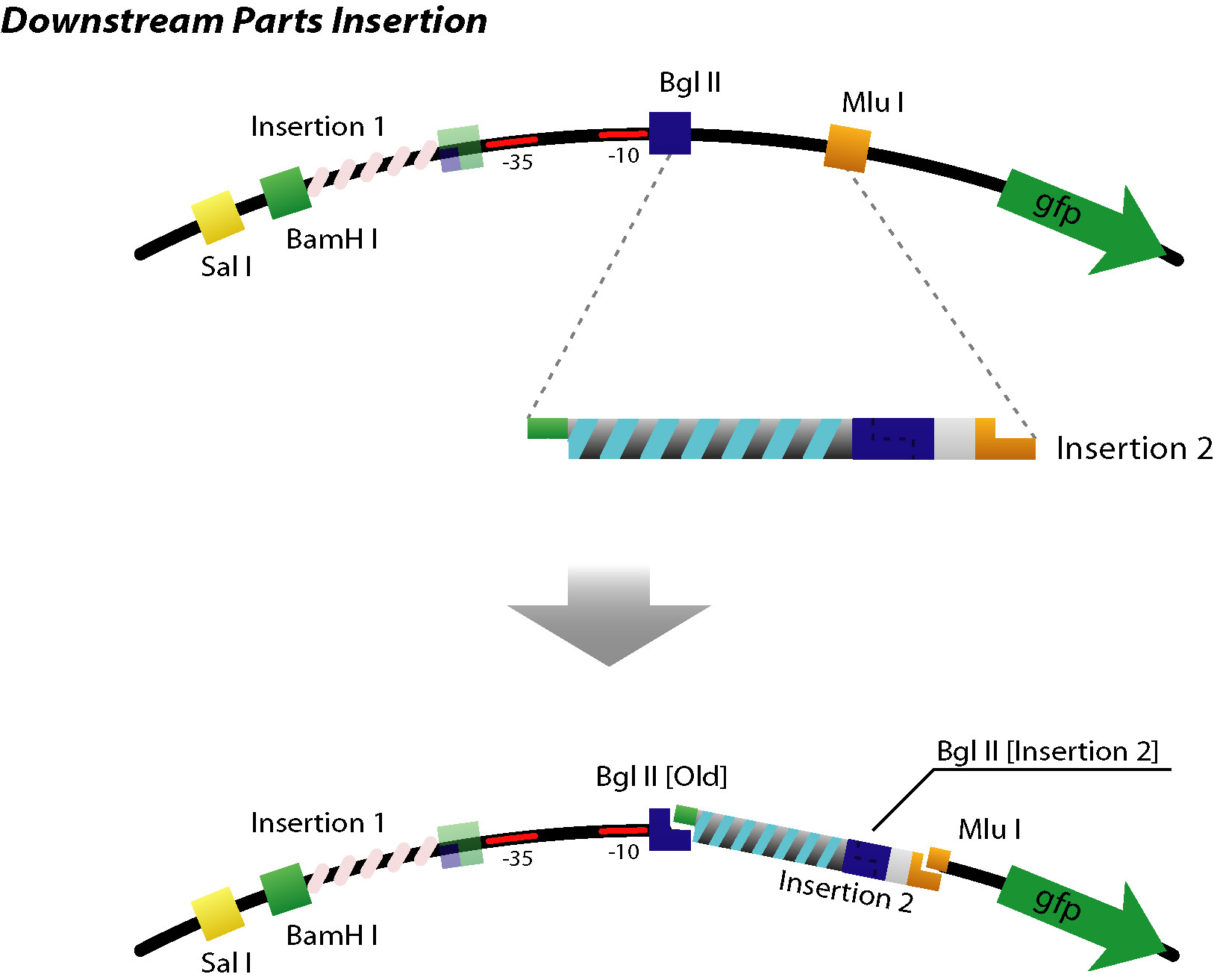
Construction Phase
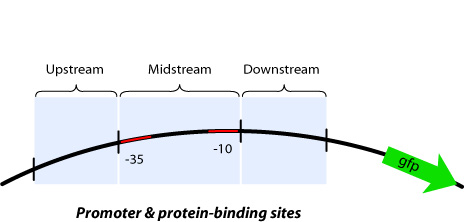
Up/Mid/Downstream
working model
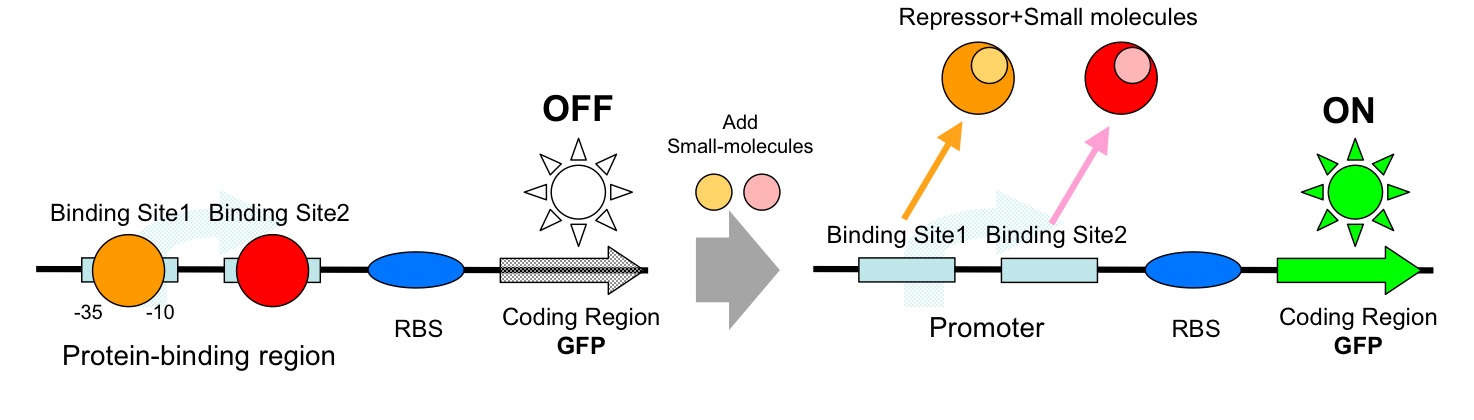
- AND Gate (Repressor+Repressor)
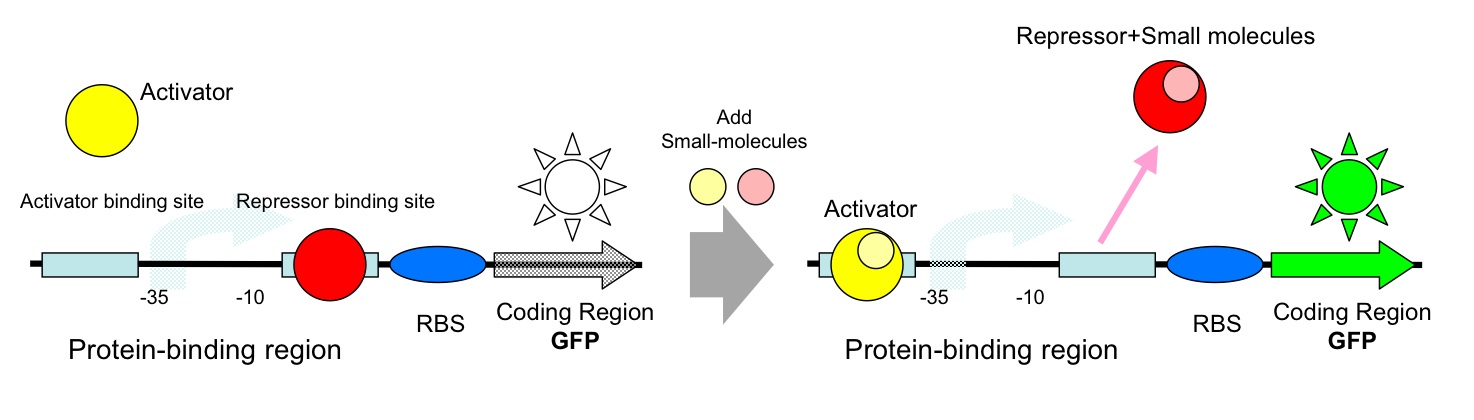
- AND Gate (Activator+Repressor)
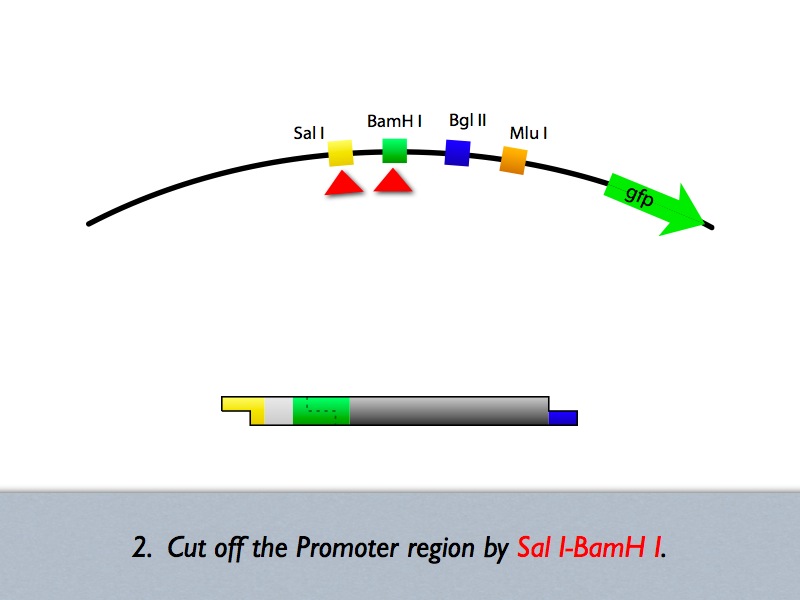
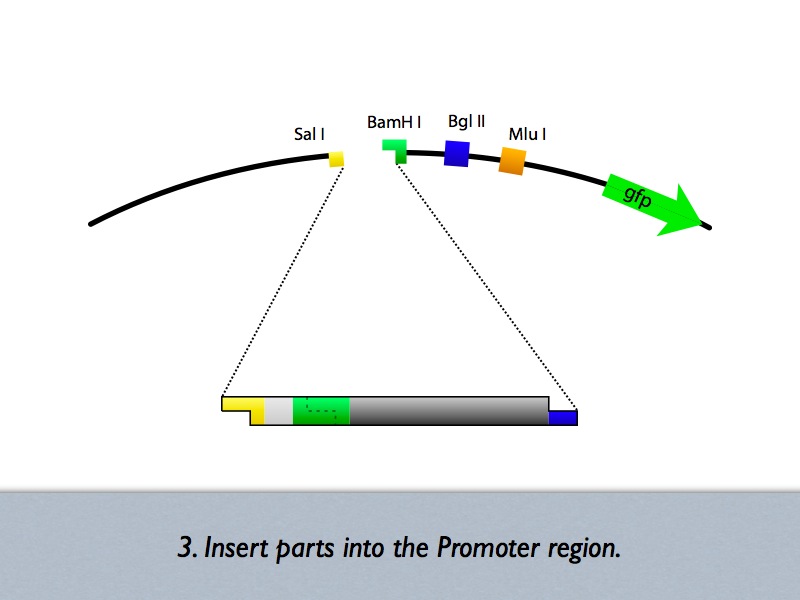
DNA Construction Procedure
- Midstream Parts Insertion
- [http://131.112.128.86/downloads/tokyo_mid_insertion.mov Midstream Parts Insertion Procedure (.mov)] (Requires QuickTime)
- Up/Downstream Parts Insertion
- Next parts can be inserted with the same procedure. (Up/Downstream Insertion Parts)