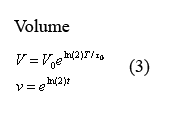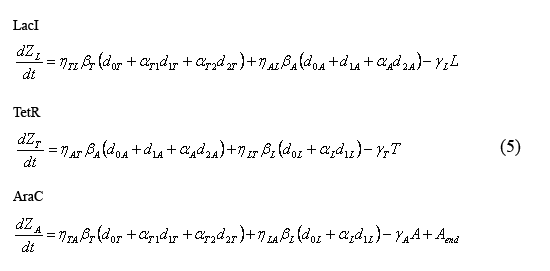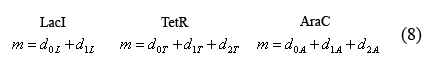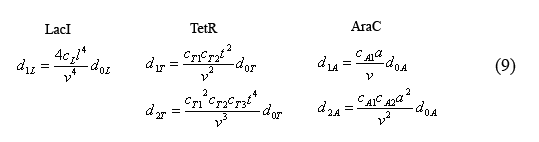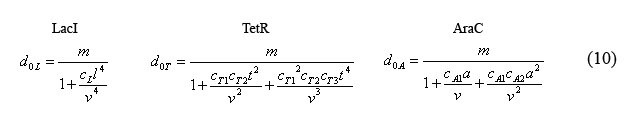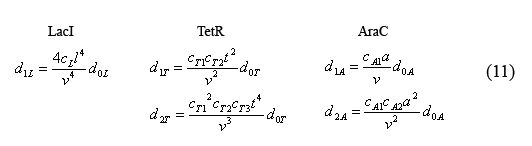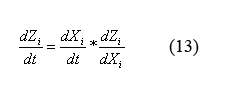Derivation of the Model Equations

From 2006.igem.org

Revision as of 06:50, 1 November 2006

Derivation of the model equations

The chemical reactions describing the tri-stable switch can be divided into the two categories of fast and slow reactions. Fast reactions such as dimer formation and promoter-binding occur in the scale of seconds and are therefore modeled to be in equilibrium. Conversely, slow reactions including the likes of transcription, translation, and protein degradation occur on the scale of minutes and are thus modeled to be evolving with time.

Fast reversible reaction equations

The following equations (1) describe the fast reactions. The characters L,T,A denote molecules of LacI, TetR, and, AraC, respectively while the subscripts denote whether the molecule is a monomer (blank), dimer(2), tri-mer(3), etc. The k's denote reaction rates.

Note that the equations include volume explicitly. Cell volume is modeled in this way as it is a slowly evolving function of time.

Slow irreversible reaction equations

The following equations (2) describe the slow irreversible reactions of transcription and translation (both taken into account with the reaction rate kti) and protein degradation (reaction constant kdi). The coefficients eta-ij take into account the relative translation rates of proteins from the same transcripts. For eta-ij, "i" represents the promoter responsible for producing the molecule and "j" represents the molecule being translated [ex: eta-LA corresponds to the relative rate of AraC production from the trascript produced by the LacI promoter]. To establish a convention, eta's are relative to the translation rate of the first gene on a particular transcript. Thus eta for the first gene on the mRNA transcript = 1. The alpha-i coefficients represent relative transcription rates. In this case, "i" denotes the promoter from which the mRNA is transcribed.

Equations governing cell volume

The following two equations (3) describing cellular growth and division are taken directly from the aforementioned paper by Isaacs et al. The first equation describes the volume increase from the time immediately following cell division to the time immediately before it. In this equation, V0 denotes the volume of the cell at the beginning of growth and T0 denotes the time of cell division. In our model at times T=q*t0 in which q is an integer, we have volume V and protein concentration n halve - thus modeling volume division and the resulting protein redistribution. The second equation describes the dimensionless equation in which t is measured in terms of fcell-division time and the cell volume changes between 1 and 2.

Equations for the total number of molecules

The following equations (4) describe the total number of inhibitor protein molecules zi. d#i represents the number, "#", of molecules bound to the "i" promoter. (ex: all of the LacI tetramers bound to pLacI promoters are accounted for by the 4d1L term.)

Equations describing the temporal evolution of the total number inhibitor molecules

The following equations (5) describe the temporal evolution of the total number of inhibitor molecules. Beta-i = the cell division time multiplied by the combined transcription and translation rates from a given promoter "i" (t0*kti), thus representing the total number of protein molecules maximally produced by a given promoter. Similarly, Gamma-i = the cell division time multiplied by the degradation rate of protein i (t0*kdi), thus representing the total number of protein i destabilized over one cell division time. The eta and alpha terms are described in the section above describing the equations for the slow reactions. Note that the equation describing the temporal evolution of AraC includes the term "Aend." This term represents the endogenous expression of AraC in dH5alpha's. Our preliminary work suggests that this endogenous AraC has very little effect on our pBad promoter.

Fast reaction equilibrium equations

Compared to the slowly evolving reactions(2) described by the above equations (5), the fast reactions (1) can be considered to be in equilibrium. Thus the following equilibrium relations (6) hold.

Equations modeling the presence of the inducers

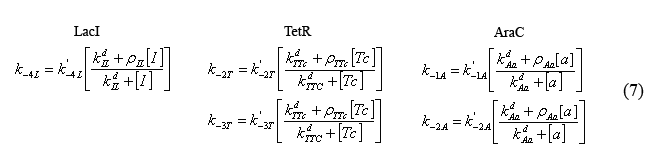
The following equations (7) model the effect of the chemical inducers on the system. The model regards the proteins bound to the inducers as having increased dissociation rates (ki-#) as specified below. The reaction rate with the apostrophe denotes the original reaction rate in the absence of inducer inclusion. In these equations "I" denotes IPTG, "a" denotes arabinose, and "Tc" denotes tetracycline (or analogue aTc). The concept for and the form of these equations are based on equations described in the supplementary Information for "A bottom-up approach to gene regulation" by Guido et al. Much like the aforementioned paper by Isaacs et al., 'Bottom-up' has an extensive and brilliantly articulate derivation supplement.

Equations relating plasmid copy number to operator sites

The following equations (8) relate the plasmid copy number, "m", to the number of promoters with bound and unbound operators. As each plasmid contains 1 of each promoter, m is constant for all three promoter types.

Simplified fast reaction equilibrium equations

The equilibrium equations governing the fast reactions (6) can be simplified by defining dimensionless equilibrium constants in the form of cij=kij/(k(-ij)*V0*A) in which A is Avogadro's number. The cL's are further simplified by defining the constant cL=c1L*c2L*c3L*c4L. Additionally by plugging in successive terms we were able to write the operator equations in terms of d0L.

Equations for the number of unbound operators

Combining equations (8) and the above simplified equilibrium equations(9), we are able to solve for the number of unbound operators d0i.

Equations for the number of bound operators

By plugging the d0i's (10) back into the equations for bound operators (9), we can solve for these equations in terms of monomer concentrations.

Equation manipulations to determine change in protein monomers per time

Next we can rewrite the equations describing the temporal evolution of the total number inhibitor molecules (5) in terms of equations (10) and (11). This yields the somewhat complex equations (12) which are solely in terms of monomer protein concentration.

Equations for the change in protein monomers per time

By applying the simple mathematical manipulation (13) to equations (12) and the X derivative of equations (9) ((9) can be written in terms of X by plugging in equations (10) and (11)) we can solve for the following equations for the evolution of protein monomers as a function of time (14). I will spare you the dZi/dXi derivative equations of equation (9).

Equations describing stochastic variation

Equations for the evolution of fluorescent reporters

--Jlohmuel 03:59, 28 October 2006 (EDT)