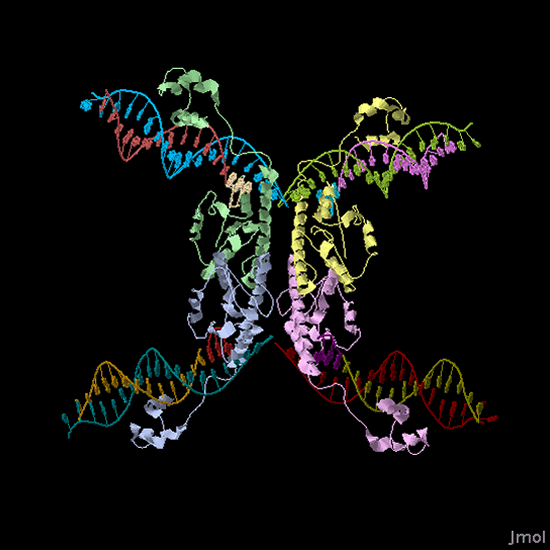Davidson 2006
From 2006.igem.org
Macampbell (Talk | contribs) |
Macampbell (Talk | contribs) |
||
| Line 8: | Line 8: | ||
{| width="900px" | {| width="900px" | ||
|- valign="top" | |- valign="top" | ||
| - | |<font size=4><div id="overview">Solving the Pancake Problem with an E. coli Computer</div></font> | + | |<font size=4><div id="overview">Solving the Pancake Problem with an <i>E. coli</i> Computer</div></font> |
[http://2006.igem.org/Image:IGEM2006_Davidson.ppt PowerPoint Presentation] and [http://2006.igem.org/Image:IGEM2006_Davidson_poster.ppt Poster] | [http://2006.igem.org/Image:IGEM2006_Davidson.ppt PowerPoint Presentation] and [http://2006.igem.org/Image:IGEM2006_Davidson_poster.ppt Poster] | ||
|- | |- | ||
Revision as of 18:41, 2 November 2006
 Project Overview [http://partsregistry.org/cgi/partsdb/pgroup.cgi?pgroup=iGEM2006partsregistry.org/cgi/partsdb/pgroup.cgi?pgroup=iGEM2006&group=Davidson Davidson Parts] Team Members Tools and Resources Check out our [http://www.bio.davidson.edu/courses/synthetic/photos/FlapJack_HotCakes.html Official Team Photo] |
The Burnt Pancake Problem
| The [http://en.wikipedia.org/wiki/Pancake_sorting pancake problem] is a puzzle in which a scrambled series of units (or stack of pancakes) must be shuffled into the correct order and orientation. You can try solving [http://www.cut-the-knot.org/SimpleGames/Flipper.shtml a simple version of the pancake problem] yourself. In the burnt pancake problem, each pancake is given an orientation by burning one side. To solve the problem, every unit, or pancake, must be placed in the proper order (largest on bottom, smallest on top) and in the proper orientation (burnt side down, golden side up). The pancakes are flipped with two spatulas: one to lift pancakes off the top of the stack, the other to flip part (or all) of the remaining stack of pancakes. The pancakes lifted by the first spatula are returned to the top of the stack without being flipped. Figure 1 illustrates how the puzzle is solved. |
Approach
| Trial and error is one approach to solving the burnt pancake problem, but how could one compute the quickest solution? Our idea is to let E. coli do the work, using each cell as a tiny processor in a massively parallel machine. A mathematical model of the flipping process helps us design the system and interpret the output of our EHOP computer. |
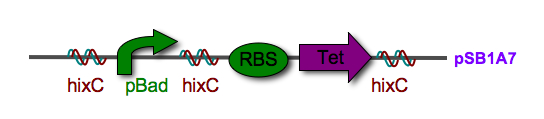
Biological System: The biological representation of a pancake is a functional unit of DNA such as a promoter or coding region. To flip these units of DNA, we have reconstituted the Hin/ Hix invertase system (Figure 2) from Salmonella typhimurium as a BioBrick compatible system in E. coli. Hin invertase () was cloned from S. typhimurium, Ames strain TA100 and tagged with LVA. We built the recombinational enhancer (RE) and Hin invertase recognition sequence HixC using the publicly available genomic sequence of S. typhimurium and [http://gcat.davidson.edu/IGEM06/oligo.html a dsDNA assembly program we created] for gene synthesis from overlapping oligos.
Every segment of DNA flanked by a pair of HixC sites is a "pancake" capable of being inverted. Hin invertase recognizes pairs of HixC sites and inverts the DNA fragment in between the two HixC sites with the help of the Fis protein bound to the RE. In our system, selectable phenotypes (including antibiotic resistance and RFP expression), depend upon the proper arrangement of a series of HixC-flanked DNA segments in a plasmid. This allows us to select for cells that have successfully solved the puzzle. An example of a sorted stack of two pancakes is shown in Figure 3. There are 7 other configurations of 2 pancakes. If we increase the number of pancakes to 4, there are 384 configurations. In general, there are 2n n! configurations of n pancakes, a combinatorial explosion of possibilities. How many should we build and test? Which ones are most informative? We need a mathematical model to help answer this question. |
|
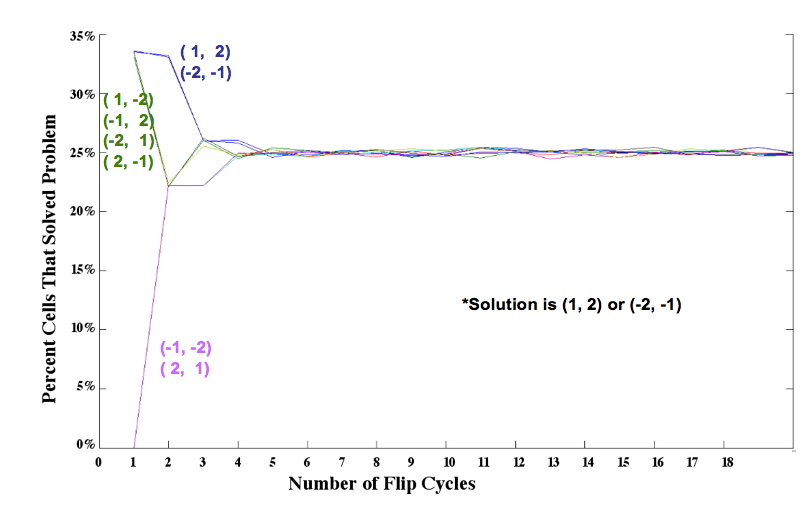
Mathematical Model: Our mathematical representation of a stack of pancakes is a signed permutation, in which each numerical value represents the pancake size and the sign of the number represents the orientation. For example, (1, 2, 3, 4) is a sorted stack of four pancakes, all in the proper order and orientation, and (-2, 4, -1, 3) is the scrambled stack of four pancakes shown on the far left of Figure 1. Note that pancakes 1 and 2 are negative, indicating that these two pancakes are in the wrong orientation (burnt side up). We simulated the flipping process by assuming that each segment of DNA flanked by Hix sites is equally likely to be flipped by Hin invertase. In an n-pancake stack, there are n+1C2 ways to choose a segment: two spatula locations must be chosen from among the n + 1 potential locations. For example, there are 5C2 = 5! 3! / 2! = 10 different ways to perform a single flip in a stack of 4 pancakes. The random flipping process continues until the stack is sorted in the correct order and orientation, or until we artificially stop the random flipping process. Figure 4 shows the percent of plasmids that we expect to be sorted after 1 flip, 2 flips, and so on, up to 20 flips, for each of the eight initial configurations.From these simulations, and similar results for stacks of 3 and 4 pancakes, we discovered that the probability of a plasmid being sorted after k flips was determined by how many ways the solution could be obtained. Several initial configurations had essentially the same graph in our simulations because they had the same number of ways of being sorted. Only one representative from each of these "families" of initial configurations needs to be built and tested. |
| Methods and Results The following is an outline of what the Davidson team will present at iGEM 2006 | |||
| Basic parts Parts used in this project were designed by two iGEM Teams
Modeling
| Building the Biological System
| Conclusions
| |
Students
- Sabriya Rosemond is a junior biology major at Hampton University.
- Erin Zwack is a junior biology major at Davidson College.
- Lance Harden is a sophomore math major at Davidson College.
- Samantha Simpson is a sophomore at Davidson College who might design a major in genomics.
Faculty
- A. Malcolm Campbell [http://www.bio.davidson.edu/campbell Department of Biology]
- Laurie J. Heyer [http://www.davidson.edu/math/heyer/ Department of Mathematics]
- Karmella Haynes [http://www.bio.davidson.edu/ Department of Biology - teaching postdoc and visiting assistant professor]
iGEM 2006 Jamboree
White Board
Biology Tools (Wet Bench)
- Pancake Parts
- Davidson Protocols
- [http://gcat.davidson.edu/IGEM06/oligo.html Oligo Cuts Optimization]: by Lance Harden
- Papers of Interest
Math Tools
- Pancake Simulators, aka The Lancelator (MATLAB Code)
- Other Flipping Simulators
- [http://gcat.davidson.edu/IGEM06/randompancakeflipper.m User-Friendly Version]
- [http://gcat.davidson.edu/IGEM06/powerflipper.m Power-User Version]
- [http://gcat.davidson.edu/IGEM06/powerflipperplus.m Power-User Update]
- [http://gcat.davidson.edu/IGEM06/findmin.m Findmin]
- [http://gcat.davidson.edu/IGEM06/bigtrial.m Bigtrial]
- Graphing Tools
- [http://gcat.davidson.edu/IGEM06/pancakeplotter.m Pancakeplotter]
- [http://gcat.davidson.edu/IGEM06/permplotter.m Permplotter]
- [http://gcat.davidson.edu/IGEM06/adjmat.m Adjmat - creates adjacency matrices]
- [http://gcat.davidson.edu/IGEM06/bioadjmat.m Bioadjmat - Adjmat with biological equivalence]
- [http://gcat.davidson.edu/IGEM06/make_radial.m Make_radial - creates a radially-embedded graph]
- [http://gcat.davidson.edu/IGEM06/find_diam.m Find_diam - finds the diameter of a pancake graph]
Bio-Math Tools
- [http://gcat.davidson.edu/IGEM06/signedperms.m Signedperms - lists all signed permutations for a stack of k pancakes]
- [http://gcat.davidson.edu/IGEM06/bioperms.m Bioperms - Signedperms with biological equivalence]
Assembly Plans
Progress